
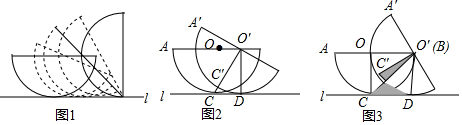
 如圖1,一個半徑為2的半圓在平面作無滑動順時針滾動,可以把平面看做直線l,初始位置的半圓O與直線l相切于點C,AB∥l,滾動過程中,半圓O′與直線l相切于點D,點A、B、C在半圓O′上的對應點分別為A′、B′、C′.
如圖1,一個半徑為2的半圓在平面作無滑動順時針滾動,可以把平面看做直線l,初始位置的半圓O與直線l相切于點C,AB∥l,滾動過程中,半圓O′與直線l相切于點D,點A、B、C在半圓O′上的對應點分別為A′、B′、C′.分析 (1)用含30°的直角三角形直接計算即可;
(2)①同(1)的方法計算即可;②利用兩次順時針滾動的角度之和即可得出結論;③分別求出扇形和三角形的面積直接比較大小和求和即可.
解答 解:(1)在Rt△CO'D中,∠C′O′D=30°,O'D=r=2,
∴O'D=$\sqrt{3}$CD,
∴CD=$\frac{2\sqrt{3}}{3}$,
(2)①∵點O′恰好經過點B.
∴OO'=O'D=OC=CD=2,
故答案為2,
②∵OO'=O'D=OC=CD=2,
∴四邊形OCDO'是菱形,
∵∠OCD=90°,
∴四邊形OCDO'是正方形,
∵O'C是對角線,
∴∠CO'D=45°,
∵∠C'O'D'=30°,
∴∠DOC'=∠CO'D+∠C'O'D'=75°,
③如圖3,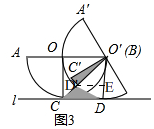 ∵∠C'O'D'=30°,
∵∠C'O'D'=30°,
∴S1=$\frac{30π•{2}^{2}}{360}$=$\frac{π}{3}$>1
過點D'作D'E⊥OD,
在Rt△O'D'E中,O'D'=2,∠EO'D'=45°,
∴O'E=$\frac{\sqrt{2}}{2}$O'D'=$\sqrt{2}$,
∴DE=O'D-O'E=2-$\sqrt{2}$,
∴S2=$\frac{1}{2}$CD•DE=$\frac{1}{2}$×2×(2-$\sqrt{2}$)=2-$\sqrt{2}$<1,
∴S1>S2,S1+S2=$\frac{π}{3}$+2-$\sqrt{2}$
故答案為:>;$\frac{π}{3}$+2-$\sqrt{2}$
點評 此題是圓的綜合題,主要考查了扇形的面積,三角形面積公式,正方形的判定,解本題的關鍵是找出順時針滾動的角度,在以往將等邊三角形滾動的題型上轉化到半圓上,是一道難度不大的好題.


科目:初中數學 來源: 題型:解答題
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
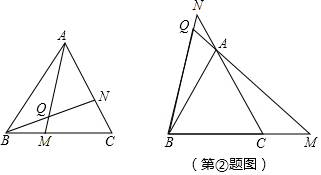
 (1)尺規作圖:作△ABC的外接圓⊙O.(保留作圖痕跡,不寫畫法)
(1)尺規作圖:作△ABC的外接圓⊙O.(保留作圖痕跡,不寫畫法)查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
科目:初中數學 來源: 題型:填空題
 如圖,點A是拋物線y=x2-4x對稱軸上的一點,連接OA,以A為旋轉中心將AO逆時針旋轉90°得到AO′,當O′恰好落在拋物線上時,點A的坐標為(2,-1)或(2,2).
如圖,點A是拋物線y=x2-4x對稱軸上的一點,連接OA,以A為旋轉中心將AO逆時針旋轉90°得到AO′,當O′恰好落在拋物線上時,點A的坐標為(2,-1)或(2,2).查看答案和解析>>
科目:初中數學 來源: 題型:解答題
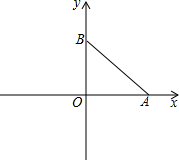 如圖,在平面直角坐標系中,O為坐標原點,A、B兩點的坐標分別為
如圖,在平面直角坐標系中,O為坐標原點,A、B兩點的坐標分別為查看答案和解析>>
科目:初中數學 來源: 題型:解答題
| 用水量/月 | 單價(元/m3) |
| 不超過20m3 | 3 |
| 超過20m3的部分 | 4 |
| 另:每立方米用水加收0.2元的城市污水處理費 | |
查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
| A. | $\frac{1}{2}$ | B. | 1 | C. | $\sqrt{2}$ | D. | $\frac{3}{2}$ |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com