
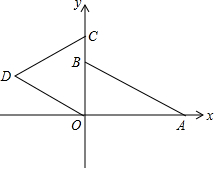
 如圖,Rt△OAB在平面直角坐標系中,點A在x軸的正半軸上,點B在y軸的正半軸上,且OA=3,OB=$\sqrt{3}$,邊長為$\frac{3\sqrt{3}}{2}$的等邊三角形OCD的一邊OC在y軸的正半軸上,點D位于第二象限內.若等邊三角形OCD以每秒1個單位的速度沿x軸的正方向運動,點D運動到y軸上則停止運動;設點O運動的對應點為點E,ED與y軸的交點為F,CD與y軸和AB的交點分別為H,G,CE與AB的交點為M,設△OCD運動的時間為t秒,△ECD與△OAB重疊部分的面積為S.
如圖,Rt△OAB在平面直角坐標系中,點A在x軸的正半軸上,點B在y軸的正半軸上,且OA=3,OB=$\sqrt{3}$,邊長為$\frac{3\sqrt{3}}{2}$的等邊三角形OCD的一邊OC在y軸的正半軸上,點D位于第二象限內.若等邊三角形OCD以每秒1個單位的速度沿x軸的正方向運動,點D運動到y軸上則停止運動;設點O運動的對應點為點E,ED與y軸的交點為F,CD與y軸和AB的交點分別為H,G,CE與AB的交點為M,設△OCD運動的時間為t秒,△ECD與△OAB重疊部分的面積為S.分析 (1)如圖1中,作DH⊥OC于H.根據等邊三角形的性質求出點D的坐標,即可解決問題.
(2)分兩種情形討論①如圖3中,當0<t≤$\frac{3}{2}$時,重疊部分是平行四邊形EFBM,②如圖4中,當$\frac{3}{2}$<t≤$\frac{9}{4}$時,重疊部分是五邊形EFHKM.分別計算即可.
(3)當△FEM是等邊三角形時,E,F,M,P為頂點的四邊形是菱形,分三種情形討論即可解決問題.
解答 解:(1)如圖1中,作DH⊥OC于H.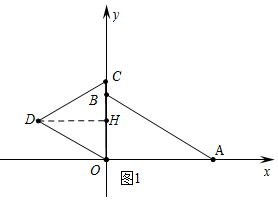
∵△ODC是等邊三角形,OC=DC=DO=$\frac{3\sqrt{3}}{2}$,
∴DH=DC•sin60°=$\frac{9}{4}$,OH=$\frac{1}{2}$OD=$\frac{3\sqrt{3}}{4}$,
∴D(-$\frac{9}{4}$,$\frac{3\sqrt{3}}{4}$),
∵反比例函數y=$\frac{k}{x}$的圖象經過點D,
∴k=-$\frac{27\sqrt{3}}{16}$.
(2)如圖2中,當直線CD經過點B時.
∵DB=DF=BF=$\frac{\sqrt{3}}{2}$,
∴DH=DB•sin60°=$\frac{3}{4}$,OE=$\frac{9}{4}$-$\frac{3}{4}$=$\frac{3}{2}$
①如圖3中,當0<t≤$\frac{3}{2}$時,重疊部分是平行四邊形EFBM,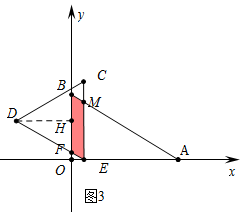
∵直線AB的解析式為y=-$\frac{\sqrt{3}}{3}$x+$\sqrt{3}$,
∵OE=t,
∴ME=-$\frac{\sqrt{3}}{3}$t+$\sqrt{3}$,
∴S=t•(-$\frac{\sqrt{3}}{3}$t+$\sqrt{3}$)=-$\frac{\sqrt{3}}{3}$t2+$\sqrt{3}$t.
②如圖4中,當$\frac{3}{2}$<t≤$\frac{9}{4}$時,重疊部分是五邊形EFHKM.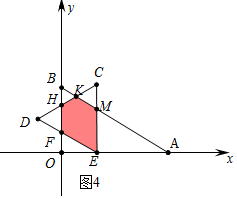
S=S△DCE-S△CKM-S△DHF=$\frac{\sqrt{3}}{4}$•($\frac{3\sqrt{3}}{2}$)2-$\frac{\sqrt{3}}{4}$•[$\frac{3\sqrt{3}}{2}$-(-$\frac{\sqrt{3}}{3}$t+$\sqrt{3}$)]2-$\frac{\sqrt{3}}{4}$($\frac{3\sqrt{3}}{2}$-$\frac{2\sqrt{3}}{3}$t)2=-$\frac{5\sqrt{3}}{12}$t2+$\frac{5\sqrt{3}}{4}$t+$\frac{3\sqrt{3}}{2}$,
綜上所述,S=$\left\{\begin{array}{l}{-\frac{\sqrt{3}}{3}{t}^{2}+\sqrt{3}t}&{(0<t≤\frac{3}{2})}\\{-\frac{5\sqrt{3}}{12}{t}^{2}+\frac{5\sqrt{3}}{4}t+\frac{3\sqrt{3}}{2}}&{(\frac{3}{2}<t≤\frac{9}{4})}\end{array}\right.$.
(3)如圖5中,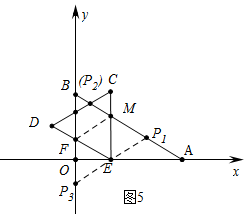
當△FEM是等邊三角形時,E,F,M,P為頂點的四邊形是菱形,
∵EF=EM,
∴$\frac{2\sqrt{3}}{3}$t=-$\frac{\sqrt{3}}{3}$t+$\sqrt{3}$,
∴t=1,
∴OE=1,OF=$\frac{\sqrt{3}}{3}$,
∵四邊形EFMP1是菱形,
∴P1(2,$\frac{\sqrt{3}}{3}$),
∵四邊形EMP2F是菱形,
∴P2(0,$\sqrt{3}$),
∵四邊形EMFP3是菱形,
∴P3(0,-$\frac{\sqrt{3}}{3}$),
綜上所述,滿足條件的點P坐標為(2,$\frac{\sqrt{3}}{3}$)或(0,$\sqrt{3}$)或(0,-$\frac{\sqrt{3}}{3}$).
點評 本題考查反比例函數綜合題、平移變換、多邊形面積、等邊三角形的性質、菱形的判定和性質等知識,解題的關鍵是學會分類討論的思想思考問題,學會利用參數構建方程解決問題,屬于中考壓軸題.


科目:初中數學 來源: 題型:選擇題
| A. | 一個有理數的絕對值一定比0大 | |
| B. | 兩個數比較大小,絕對值大的反而小 | |
| C. | 相反數等于它本身的數是0 | |
| D. | 若a>0,b<0且|a|>|b|,則a+b<0 |
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
 如圖,矩形ABCD中,AB=3,BC=4,點P在射線BC上運動,點P和點P′關于BD對稱,當P′、P、D三點共線時運動停止,連接DP′、DP.設BP=x.
如圖,矩形ABCD中,AB=3,BC=4,點P在射線BC上運動,點P和點P′關于BD對稱,當P′、P、D三點共線時運動停止,連接DP′、DP.設BP=x.查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
| A. | (-$\frac{2}{3}$)-2=$\frac{4}{9}$ | B. | $\frac{-a+b}{c}$=-$\frac{a+b}{c}$ | ||
| C. | ($\frac{2{a}^{2}}{3b}$)3=$\frac{8{a}^{5}}{9{b}^{3}}$ | D. | $\frac{-a-b}{-a+b}$=$\frac{a+b}{a-b}$ |
查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
 如圖,用16m長的鋁合金做成一個長方形的窗框.設長方形窗框的橫條長度為xm,則長方形窗框的面積為( )
如圖,用16m長的鋁合金做成一個長方形的窗框.設長方形窗框的橫條長度為xm,則長方形窗框的面積為( )| A. | x(16-x)m2 | B. | x(8-x)m2 | C. | x($\frac{16-3x}{2}$)m2 | D. | x($\frac{16-x}{2}$)m2 |
查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
| A. | 1 | B. | 2個 | C. | 3個 | D. | 4個 |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com