
 如圖2,已知△ABC中,∠ACB=90°,AC=b,BC=a.將△ABC繞點C按順時針方向旋轉90°,點B旋轉到點B′,點A旋轉到點A′.
如圖2,已知△ABC中,∠ACB=90°,AC=b,BC=a.將△ABC繞點C按順時針方向旋轉90°,點B旋轉到點B′,點A旋轉到點A′.分析 (1)根據旋轉的性質,在CB上截取CA′=CA得到點A的對應點A′,延長AC到B′使CB′=CB,則B′為點B的對應點;
(2)根據旋轉的性質得到CA′=CA=b,CB′=CB=a,∠BCB′=90°,然后根據三角形面積公式求解.
解答 解:(1)如圖,△CA′B′為所作;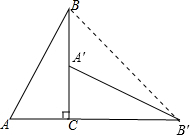
(2)∵△ABC繞點C按順時針方向旋轉90°得到△A′B′C,
∴CA′=CA=b,CB′=CB=a,∠BCB′=90°,
∴S△BB′A′=S△CBB′-S△CA′B′=$\frac{1}{2}$•a•a-$\frac{1}{2}$a•b=$\frac{1}{2}$a2-$\frac{1}{2}$ab.
點評 本題考查了作圖-旋轉變換:根據旋轉的性質可知,對應角都相等都等于旋轉角,對應線段也相等,由此可以通過作相等的角,在角的邊上截取相等的線段的方法,找到對應點,順次連接得出旋轉后的圖形.


 名師點撥卷系列答案
名師點撥卷系列答案科目:初中數學 來源: 題型:解答題
查看答案和解析>>
科目:初中數學 來源: 題型:填空題
 物理學這樣的事實:當壓力F不變時,壓強P和受力面積S之間是反比例函數,可以表示成P=$\frac{F}{S}$.一個圓臺形物體的上底面積是下底面積的$\frac{2}{3}$,如圖,如果正放在桌面上,對桌面的壓強是200Pa,翻過來放,對桌面的壓強是300Pa.
物理學這樣的事實:當壓力F不變時,壓強P和受力面積S之間是反比例函數,可以表示成P=$\frac{F}{S}$.一個圓臺形物體的上底面積是下底面積的$\frac{2}{3}$,如圖,如果正放在桌面上,對桌面的壓強是200Pa,翻過來放,對桌面的壓強是300Pa.查看答案和解析>>
科目:初中數學 來源: 題型:填空題
查看答案和解析>>
科目:初中數學 來源: 題型:填空題
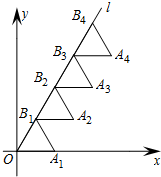 如圖,放置的△OA1B1、△B1A2B2、△B2A3B3,…,都是邊長為1的等邊三角形,點A在x軸上,點O,B1,B2,B3,…都在直線l上,則點A2015的坐標為(1008,1007$\sqrt{3}$).
如圖,放置的△OA1B1、△B1A2B2、△B2A3B3,…,都是邊長為1的等邊三角形,點A在x軸上,點O,B1,B2,B3,…都在直線l上,則點A2015的坐標為(1008,1007$\sqrt{3}$).查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com