
分析 由∠ACB=90°,CD是斜邊上的中線,求出AB=6,根據AB+AC+BC=14,求出AC+BC,根據勾股定理得出AC2+BC2=AB2=36推出AC•BC=14,根據S=$\frac{1}{2}$AC•BC即可求出答案.
解答 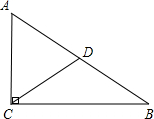 解:如圖,∵∠ACB=90°,CD是斜邊上的中線,
解:如圖,∵∠ACB=90°,CD是斜邊上的中線,
∴AB=2CD=6,
∵AB+AC+BC=14,
∴AC+BC=8,
由勾股定理得:AC2+BC2=AB2=36,
∴(AC+BC)2-2AC•BC=36,
AC•BC=14,
∴S=$\frac{1}{2}$AC•BC=7.
故答案為:7.
點評 本題主要考查對直角三角形斜邊上的中線,勾股定理,三角形的面積等知識點的理解和掌握,能根據性質求出AC•BC的值是解此題的關鍵.


 名校通行證有效作業系列答案
名校通行證有效作業系列答案科目:初中數學 來源: 題型:解答題
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
 如圖,已知在△ABC中,AD是BC邊上的中線,E是AD的中點,連接BE并延長交AC于點F,G是BF的中點.求證:
如圖,已知在△ABC中,AD是BC邊上的中線,E是AD的中點,連接BE并延長交AC于點F,G是BF的中點.求證:查看答案和解析>>
科目:初中數學 來源: 題型:解答題
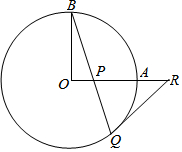 如圖,OA和OB是⊙O的半徑,并且OA⊥OB.P是OA上任意一點,BP的延長線交⊙O于點Q,點R在OA的延長線上,且RP=RQ.
如圖,OA和OB是⊙O的半徑,并且OA⊥OB.P是OA上任意一點,BP的延長線交⊙O于點Q,點R在OA的延長線上,且RP=RQ.查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
 如圖,點A、B、C、P在⊙O上,CD⊥OA,CE⊥OB,垂足分別為D,E,∠DCE=40°,則∠P的度數為( )
如圖,點A、B、C、P在⊙O上,CD⊥OA,CE⊥OB,垂足分別為D,E,∠DCE=40°,則∠P的度數為( )| A. | 70° | B. | 60° | C. | 40° | D. | 35° |
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
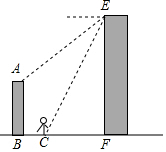 為紀念京漢鐵路工人大罷工而修建的二七紀念塔于去年下半年重新整修,一裝修工在塔EF的頂部處測得對面一棟AB=9米高的樓房頂部A的俯角為45°,測得樓房正前方BC=7米處一站牌底部C點的俯角為60°,請你幫助裝修工人計算塔的高度是多少?($\sqrt{3}$≈1.732,結果保留到1米.)
為紀念京漢鐵路工人大罷工而修建的二七紀念塔于去年下半年重新整修,一裝修工在塔EF的頂部處測得對面一棟AB=9米高的樓房頂部A的俯角為45°,測得樓房正前方BC=7米處一站牌底部C點的俯角為60°,請你幫助裝修工人計算塔的高度是多少?($\sqrt{3}$≈1.732,結果保留到1米.)查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com