
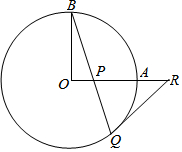
 如圖,OA和OB是⊙O的半徑,并且OA⊥OB.P是OA上任意一點(diǎn),BP的延長(zhǎng)線交⊙O于點(diǎn)Q,點(diǎn)R在OA的延長(zhǎng)線上,且RP=RQ.
如圖,OA和OB是⊙O的半徑,并且OA⊥OB.P是OA上任意一點(diǎn),BP的延長(zhǎng)線交⊙O于點(diǎn)Q,點(diǎn)R在OA的延長(zhǎng)線上,且RP=RQ.分析 (1)連接OQ.欲證明RQ是⊙O的切線,只要證明∠OQR=90°.
(2)求出兩個(gè)特殊位置的∠B的值即可解決問題.
(3)如圖2中,延長(zhǎng)AO交⊙于M.由PA•PM=PB•PQ(相交弦定理,也可以連接BM、AQ證明△PBM∽△PAQ得到),推出(OB-OP)(OB+OP)=PB•PQ,可得OB2-OP2=PB•PQ.
解答 (1)證明:連接OQ.
∵OA⊥OB,
∴∠2+∠B=90°,
∵OB=OQ,
∴∠B=∠4,
∵RP=RQ,
∴∠1=∠3=∠2,
∴∠3+∠4=90°,
∴OQ⊥RQ,
∴RQ是⊙O的切線.
(2)解:如圖1中,
①當(dāng)點(diǎn)R與A重合時(shí),易知∠B=45°.
②當(dāng)AR=OA時(shí),在Rt△ORQ中,∵∠OQR=90°,OR=2OQ,
∴∠R=30°,
∵RQ=RP,
∴∠RPQ=∠RQP=75°,
∴∠OPB=75°,
∴∠B=90°-∠OPB=15°,
綜上所述,15°≤∠B<45°.
(3)如圖2中,延長(zhǎng)AO交⊙于M.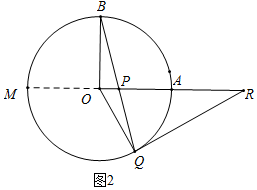
∵PA•PM=PB•PQ(相交弦定理,也可以連接BM、AQ證明△PBM∽△PAQ得到),
∴(OB-OP)(OB+OP)=PB•PQ,
∴OB2-OP2=PB•PQ.
即OB2=PB•PQ+OP2.
點(diǎn)評(píng) 本題考查圓綜合題、切線的判定和性質(zhì)、等腰三角形的性質(zhì)、相交弦定理等知識(shí),解題的關(guān)鍵是靈活運(yùn)用所學(xué)知識(shí)解決問題,屬于中考?jí)狠S題.



| 年級(jí) | 高中課程 | 年級(jí) | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:初中數(shù)學(xué) 來源: 題型:解答題

查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:解答題
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:填空題
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:解答題
 用40cm長(zhǎng)的繩子圍成矩形ABCD,設(shè)AB=xm,矩形ABCD的面積為S(m2)
用40cm長(zhǎng)的繩子圍成矩形ABCD,設(shè)AB=xm,矩形ABCD的面積為S(m2)| x | … | 8 | 9 | 9.5 | 10 | 10.5 | 11 | 12 | … |
| S | … | 96 | 99 | 99.75 | 100 | 99,75 | 99 | 96 | … |
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:選擇題
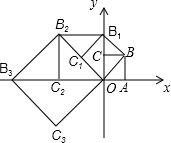 如圖,在平面直角坐標(biāo)系中有一邊長(zhǎng)為1的正方形OABC,邊OA、OC分別在x軸、y軸上,如果以對(duì)角線OB為邊作第二個(gè)正方形OBB1C1,再以對(duì)角線OB1為邊作第三個(gè)正方形OB1B2C2,照此規(guī)律作下去,則點(diǎn)B2015的坐標(biāo)為( )
如圖,在平面直角坐標(biāo)系中有一邊長(zhǎng)為1的正方形OABC,邊OA、OC分別在x軸、y軸上,如果以對(duì)角線OB為邊作第二個(gè)正方形OBB1C1,再以對(duì)角線OB1為邊作第三個(gè)正方形OB1B2C2,照此規(guī)律作下去,則點(diǎn)B2015的坐標(biāo)為( )| A. | (21008,0) | B. | (21007,-21007) | C. | (21009,21009) | D. | (-21007,21007) |
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:填空題
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:解答題
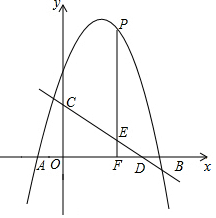 如圖,拋物線y=-x2+4x+5與x軸交于A,B兩點(diǎn)(點(diǎn)A在點(diǎn)B的左側(cè)),直線y=$-\frac{3}{4}x+3$與y軸交于點(diǎn)C,與x軸交于點(diǎn)D.P是x軸上方的拋物線上一動(dòng)點(diǎn),過點(diǎn)P作PF⊥x軸于點(diǎn)F,交直線CD于點(diǎn)E,設(shè)點(diǎn)P的橫坐標(biāo)為m.
如圖,拋物線y=-x2+4x+5與x軸交于A,B兩點(diǎn)(點(diǎn)A在點(diǎn)B的左側(cè)),直線y=$-\frac{3}{4}x+3$與y軸交于點(diǎn)C,與x軸交于點(diǎn)D.P是x軸上方的拋物線上一動(dòng)點(diǎn),過點(diǎn)P作PF⊥x軸于點(diǎn)F,交直線CD于點(diǎn)E,設(shè)點(diǎn)P的橫坐標(biāo)為m.查看答案和解析>>
百度致信 - 練習(xí)冊(cè)列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺(tái) | 網(wǎng)上有害信息舉報(bào)專區(qū) | 電信詐騙舉報(bào)專區(qū) | 涉歷史虛無主義有害信息舉報(bào)專區(qū) | 涉企侵權(quán)舉報(bào)專區(qū)
違法和不良信息舉報(bào)電話:027-86699610 舉報(bào)郵箱:58377363@163.com