
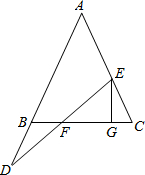
 如圖,在△ABC中,AB=AC,點(diǎn)E在線段AC上,D在AB的延長線上,連接DE交BC于F,過E作EG⊥BC于G.
如圖,在△ABC中,AB=AC,點(diǎn)E在線段AC上,D在AB的延長線上,連接DE交BC于F,過E作EG⊥BC于G.分析 (1)條件是①DB=EC,結(jié)論是②DF=EF.(也可以填條件是②,結(jié)論是①).只要證明△FBD≌△FHE,即可解決問題.
(2)由(1)可知,EH=EC,EG⊥HC,推出GH=GC,由△BFD≌△FHE,推出BF=FH,即可推出FG=FH+HG=$\frac{1}{2}$BH+$\frac{1}{2}$HC=$\frac{1}{2}$(BH+HC)=$\frac{1}{2}$BC.
解答 (1)解:條件是①DB=EC,結(jié)論是②DF=EF.(也可以填條件是②,結(jié)論是①).
理由:如圖作,EH∥AD交BC于H.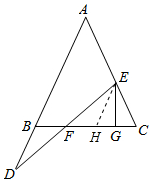
∵EH∥AD,
∴∠ABC=∠EHC,∠D=∠HEF,
∵AB=AC,
∴∠ABC=∠C=∠EHC,
∴EH=EC=BD,
在△FBD和△FEH中,
$\left\{\begin{array}{l}{∠D=∠HEF}\\{∠DFB=∠EFH}\\{BD=EH}\end{array}\right.$,
∴△FBD≌△FHE,
∴DF=EF.
(2)證明:由(1)可知,EH=EC,EG⊥HC,
∴GH=GC,
∵△BFD≌△FHE,
∴BF=FH,
∴FG=FH+HG=$\frac{1}{2}$BH+$\frac{1}{2}$HC=$\frac{1}{2}$(BH+HC)=$\frac{1}{2}$BC.
點(diǎn)評 本題考查全等三角形的判定和性質(zhì)、等腰三角形的性質(zhì)和判定等知識,解題的關(guān)鍵是學(xué)會(huì)添加常用輔助線,構(gòu)造全等三角形解決問題,屬于中考常考題型.



| 年級 | 高中課程 | 年級 | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:初中數(shù)學(xué) 來源: 題型:解答題
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:解答題

查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:解答題
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:填空題
 如圖,在一次數(shù)學(xué)活動(dòng)課上,小明用18個(gè)棱長為1的正方體積木搭成一個(gè)幾何體,然后他請小亮用其他棱長為1的正方體積木在旁邊再搭一個(gè)幾何體,使小亮所搭幾何體恰好和小明所搭幾何體拼成一個(gè)無空隙的大長方體(不改變小明所搭幾何體的形狀).
如圖,在一次數(shù)學(xué)活動(dòng)課上,小明用18個(gè)棱長為1的正方體積木搭成一個(gè)幾何體,然后他請小亮用其他棱長為1的正方體積木在旁邊再搭一個(gè)幾何體,使小亮所搭幾何體恰好和小明所搭幾何體拼成一個(gè)無空隙的大長方體(不改變小明所搭幾何體的形狀).查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:解答題
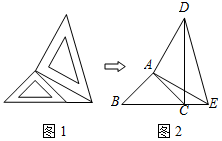 兩個(gè)大小不同的等腰直角三角形三角板如圖1所示放置,圖2是由它抽象出的幾何圖形,B,C,E在同一條直線上,連結(jié)DC.
兩個(gè)大小不同的等腰直角三角形三角板如圖1所示放置,圖2是由它抽象出的幾何圖形,B,C,E在同一條直線上,連結(jié)DC.查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:選擇題
 如圖,AB=AC,BE⊥AC于點(diǎn)E,CF⊥AB于點(diǎn)F,BE、CE相交于點(diǎn)D,則①△ABE≌△ACF,②△BDF≌CDE,③點(diǎn)D在∠BAC的平分線上,以上結(jié)論正確的是( )
如圖,AB=AC,BE⊥AC于點(diǎn)E,CF⊥AB于點(diǎn)F,BE、CE相交于點(diǎn)D,則①△ABE≌△ACF,②△BDF≌CDE,③點(diǎn)D在∠BAC的平分線上,以上結(jié)論正確的是( )| A. | ① | B. | ② | C. | ①② | D. | ①②③ |
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:填空題
 如圖,在△ABC中,AD⊥BC,CE⊥AB,垂足分別為點(diǎn)D、E.若BE=2AE,AD=3,tan∠BCE=$\frac{\sqrt{3}}{3}$,則CE=4.
如圖,在△ABC中,AD⊥BC,CE⊥AB,垂足分別為點(diǎn)D、E.若BE=2AE,AD=3,tan∠BCE=$\frac{\sqrt{3}}{3}$,則CE=4.查看答案和解析>>
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺(tái) | 網(wǎng)上有害信息舉報(bào)專區(qū) | 電信詐騙舉報(bào)專區(qū) | 涉歷史虛無主義有害信息舉報(bào)專區(qū) | 涉企侵權(quán)舉報(bào)專區(qū)
違法和不良信息舉報(bào)電話:027-86699610 舉報(bào)郵箱:58377363@163.com