
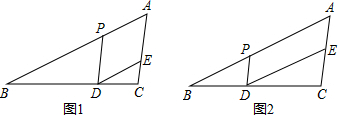
分析 (1)先判斷出四邊形APDE是平行四邊形,得出DE=AP,再由全等三角形的性質建立方程求解即可;
(2)先判斷出△CDE∽△CBA,得出CE=$\frac{1}{2}$t,再利用菱形的性質得出AP=AE,建立方程求解即可;
(3)借助(2)得出△CDE∽△CBA,利用相似三角形的面積比等于相似比的平方得出S△CED=$\frac{{t}^{2}}{5}$,同理得出S△DPB=$\frac{(10-t)^{2}}{5}$,最后用面積的差得出S=-$\frac{2}{5}$(t-5)2+10(0<t<10),即可確定出結論.
解答 解:(1)由運動知,AP=t,
∵AB=10,
∴BP=10-t,
∵DP∥AC,DE∥AB,
∴四邊形APDE是平行四邊形,
∴DE=AP,
∵△PBD≌△EDC,
∴BP=DE,
∴BP=AP,
∴t=10-t,
∴t=5,
故答案為5;
(2)由(1)知,AP=DE=t,
∵DE∥AB,
∴△CDE∽△CBA,
∴$\frac{DE}{AB}=\frac{CE}{AC}$,
∵AB=10,AC=5,
∴CE=$\frac{1}{2}$t,
∴AE=AC-CE=5-$\frac{1}{2}$t,
∵四邊形APDE是菱形,
∴AP=AE,
∴t=5-$\frac{1}{2}$t,
∴t=$\frac{10}{3}$;
(3)S有最大值,理由如下:
∵DE∥AB,
∴△CDE∽△CBA,
∴$\frac{{S}_{△CED}}{{S}_{△CAB}}=(\frac{ED}{AB})^{2}$=$(\frac{t}{10})^{2}$=$\frac{{t}^{2}}{100}$,
∵S△CAB=20,
∴S△CED=$\frac{{t}^{2}}{100}$×S△CAB=$\frac{{t}^{2}}{5}$,
同理:S△DPB=$\frac{(10-t)^{2}}{5}$,
∴S=S△CAB-S△CED-S△DPB
=20-$\frac{{t}^{2}}{5}$-$\frac{(10-t)^{2}}{5}$
=-$\frac{2}{5}$(t-5)2+10(0<t<10)
當t=5時,S最大=10.
即:S有最大值,最大值為10.
點評 此題是四邊形綜合題,主要考查了平行四邊形的判定和性質,相似三角形的判定和性質,全等三角形的性質,菱形的性質,解(2)的關鍵是得出AE=5-$\frac{1}{2}$t,解(3)的關鍵是利用相似三角形的想得出S△CED=$\frac{{t}^{2}}{5}$,S△DPB=$\frac{(10-t)^{2}}{5}$,本題體現了方程的思想,屬于中考壓軸題.


科目:初中數學 來源: 題型:解答題
| 排數 | 第1排 | 第2排 | 第3排 | 第4排 | … | 第n排 |
| 座位數 | 24 | 24+a | 24+2a | 24+3a | … | 24+(n-1)a |
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
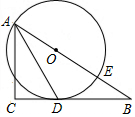 如圖,已知△ABC為直角三角形,∠C=90°,邊BC是⊙0的切線,切點為D,AB經過圓心O并與圓相交于點E,連接AD.
如圖,已知△ABC為直角三角形,∠C=90°,邊BC是⊙0的切線,切點為D,AB經過圓心O并與圓相交于點E,連接AD.查看答案和解析>>
科目:初中數學 來源: 題型:填空題
 二次函數y=ax2+bx+c(a≠0)的圖象如圖(虛線部分為對稱軸),給出以下5個結論:①x≤1時,y隨x的增大而增大;②abc>0;③b<a+c;④4a+2b+c>0;⑤3a-b<0,其中正確的結論有①④⑤(填上所有正確結論的序號).
二次函數y=ax2+bx+c(a≠0)的圖象如圖(虛線部分為對稱軸),給出以下5個結論:①x≤1時,y隨x的增大而增大;②abc>0;③b<a+c;④4a+2b+c>0;⑤3a-b<0,其中正確的結論有①④⑤(填上所有正確結論的序號).查看答案和解析>>
科目:初中數學 來源: 題型:填空題
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
 已知:如圖,AB是⊙O的直徑,點C是⊙O上一點,弧CF=弧CB,過點C作AB的垂線,垂足為D,連接BC、AC、BF,BF與C交于點E.
已知:如圖,AB是⊙O的直徑,點C是⊙O上一點,弧CF=弧CB,過點C作AB的垂線,垂足為D,連接BC、AC、BF,BF與C交于點E.查看答案和解析>>
科目:初中數學 來源: 題型:填空題
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
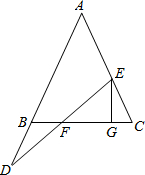 如圖,在△ABC中,AB=AC,點E在線段AC上,D在AB的延長線上,連接DE交BC于F,過E作EG⊥BC于G.
如圖,在△ABC中,AB=AC,點E在線段AC上,D在AB的延長線上,連接DE交BC于F,過E作EG⊥BC于G.查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com