
 已知:如圖,AB是⊙O的直徑,點C是⊙O上一點,弧CF=弧CB,過點C作AB的垂線,垂足為D,連接BC、AC、BF,BF與C交于點E.
已知:如圖,AB是⊙O的直徑,點C是⊙O上一點,弧CF=弧CB,過點C作AB的垂線,垂足為D,連接BC、AC、BF,BF與C交于點E.分析 (1)延長CD交O于點R.根據垂徑定理得到$\widehat{BC}$=$\widehat{BR}$,于是得到$\widehat{CF}$=$\widehat{BR}$,即可得到結論;
(2)由∠A=∠BCD,得到tanA=tan∠BCD,根據射影定理得到CD2=AD•BD=4,根據勾股定理得到AC=2$\sqrt{5}$,根據三角函數的定義即可得到結論.
解答 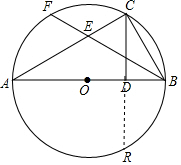 解:(1)延長CD交O于點R.
解:(1)延長CD交O于點R.
∵AB⊥CD,
∴$\widehat{BC}$=$\widehat{BR}$,
∵$\widehat{CF}$=$\widehat{BC}$.
∴$\widehat{CF}$=$\widehat{BR}$,
∴∠DCB=∠EBC;
(2)∵∠A=∠BCD,
∴tanA=tan∠BCD,
∵AB是⊙O的直徑,CD⊥AB,
∴∠ACB=90°,
∴CD2=AD•BD=4,
∵Rt△CBD中:BC2=CD2+DB2,∴BC=$\sqrt{5}$,
Rt△ACB中:AC2=AB2-BC2,
∴AC=2$\sqrt{5}$,
∴tanA=$\frac{BC}{AC}$=$\frac{1}{2}$,
∴Rt△CEB中:CE=BC•tan∠EBC=$\frac{\sqrt{5}}{2}$.
點評 本題考查了圓周角定理,勾股定理,三角函數的定義,正確的作出輔助線是解題的關鍵.


 名師伴你成長課時同步學練測系列答案
名師伴你成長課時同步學練測系列答案科目:初中數學 來源: 題型:選擇題
| A. | -2010 | B. | -2009 | C. | -2008 | D. | 2008 |
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
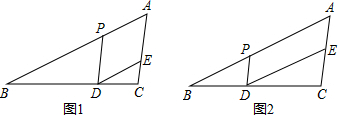
 如圖,在△ABC中,∠ABC=90°,BC=3,D為AC延長線上一點,AC=3CD,過點D作DH∥AB,交BC的延長線于點H,求BD•cos∠HBD的值.
如圖,在△ABC中,∠ABC=90°,BC=3,D為AC延長線上一點,AC=3CD,過點D作DH∥AB,交BC的延長線于點H,求BD•cos∠HBD的值.查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
科目:初中數學 來源: 題型:解答題

查看答案和解析>>
科目:初中數學 來源: 題型:解答題

查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
 如圖,AB=AC,BE⊥AC于點E,CF⊥AB于點F,BE、CE相交于點D,則①△ABE≌△ACF,②△BDF≌CDE,③點D在∠BAC的平分線上,以上結論正確的是( )
如圖,AB=AC,BE⊥AC于點E,CF⊥AB于點F,BE、CE相交于點D,則①△ABE≌△ACF,②△BDF≌CDE,③點D在∠BAC的平分線上,以上結論正確的是( )| A. | ① | B. | ② | C. | ①② | D. | ①②③ |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com