

分析 (1)按拋物線的頂點坐標設出解析式,再將點N坐標代入即可;
(2)先確定出直線AN解析式,進而表示出點F,即可得出正方形的邊長,再表示出點G坐標,最后分三種情況用兩邊相等建立方程求解即可.
(3)存在.如圖設T(x1,y1),Q(x2,y2),分別過T、Q作TE⊥y軸,QG⊥x軸,聯立直線TQ解析式與拋物線解析式,可得x1,y1,x2,y2之間的關系,當以線段TQ為直徑的圓恰好過坐標原點時,∠TOQ=90°,利用互余關系可證△TOE∽△QOG,利用相似比得出線段關系,結合x1,y1,x2,y2之間的關系求m的值
解答 解:(1)∵拋物線的頂點M的坐標為(1,4),
∴設拋物線的解析式為y=a(x-1)2+4,
∵拋物線經過點N(2,3),
∴3=a(2-1)2+4,
∴a=-1,
∴拋物線的解析式為y=-(x-1)2+4=-x2+2x+3,
(2)由(1)知,拋物線的解析式為y=-x2+2x+3,
當x=0時,y=3,
∴C(0,3),
當y=0時,0=-x2+2x+3,
∴x=-1或x=3,
∴A(-1,0),B(3,0),
∵N(2,3),
∴直線AN的解析式為y=x+1,
∵K作KF⊥AB交射線AN于點F,設點K的坐標為(t,0)(t>0),
∴F(t,t+1),
∴FK=t+1,
∵以KF為一邊在KF的右側作正方形KFGH,
∴H(2t+1,0),G(2t+1,t+1),
∵C(0,3),
∴OC=3,OG2=(2t+1)2+(t+1)2,CG2=(2t+1)2+(t+1-3)2,
∵△OCG為等腰三角形,
∴①當OC=OG時,
∴OC2=OG2,
∴9=((2t+1)2+(t+1)2,
∴t=$\frac{-3-2\sqrt{11}}{5}$(不符合題意,舍)或t=$\frac{-3+2\sqrt{11}}{5}$,
∴t+1=$\frac{2+2\sqrt{11}}{5}$,
∴正方形KFGH的邊長為$\frac{2+2\sqrt{11}}{5}$,
②當OC=CG時,
∴OC2=CG2,
∴9=(2t+1)2+(t+1-3)2,
∴t=-$\frac{\sqrt{5}}{5}$(不符合題意,舍)或t=$\frac{\sqrt{5}}{5}$,
∴t+1=$\frac{5+\sqrt{5}}{5}$,
∴正方形KFGH的邊長為$\frac{5+\sqrt{5}}{5}$,
③當OG=CG時,
∴OG2=CG2,
∴((2t+1)2+(t+1)2=(2t+1)2+(t+1-3)2,
∴t=$\frac{1}{2}$,
∴t+1=$\frac{3}{2}$,
∴正方形KFGH的邊長為$\frac{3}{2}$.
即:正方形KFGH的邊長為$\frac{2+2\sqrt{11}}{5}$或$\frac{5+\sqrt{5}}{5}$或$\frac{3}{2}$.
(3)存在.
如圖設T(x1,y1),Q(x2,y2),分別過T、Q作TE⊥y軸,QG⊥x軸,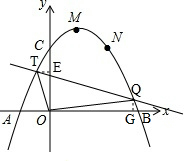
聯立$\left\{\begin{array}{l}{y=-{x}^{2}+2x+3}\\{y=mx+2}\end{array}\right.$,
解得:x2+(m-2)x-1=0,
則x1+x2=2-m,x1x2=-1,
當以線段TQ為直徑的圓恰好過坐標原點時,∠TOQ=90°,
則∠TOE+∠EOQ=∠EOQ+∠QOB=90°,
則∠TOE=∠QOB,而∠TEO=∠QGO=90°,
所以,△TOE∽△QOG,
則$\frac{TE}{QG}$=$\frac{OE}{OG}$,
即$\frac{-{x}_{1}}{{y}_{2}}$=$\frac{{y}_{1}}{{x}_{2}}$,
x1x2+y1y2=0,-1+(mx1+2)(mx2+2)=0,
-1+m2x1x2+2m(x1+x2)+4=0,
-1-m2+2m(2-m)+4=0,整理,得3m2-4m-3=0,
解得:m=$\frac{2±\sqrt{13}}{3}$.
點評 此題是二次函數綜合題,主要考查了待定系數法、正方形的性質、等腰三角形的性質相似三角形的判定與性質等知識點,解題的關鍵是根據等腰三角形的性質分類討論和相似三角形的判定與性質.


科目:初中數學 來源: 題型:解答題
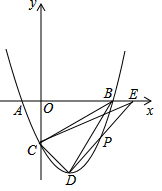 如圖,在平面直角坐標系中,二次函數y=x2-2x-3的圖象與x軸交于A,B兩點,與y軸交于點C,連接BC,點D位拋物線的頂點,點P是第四象限的拋物線上的一個動點(不與點D重合).
如圖,在平面直角坐標系中,二次函數y=x2-2x-3的圖象與x軸交于A,B兩點,與y軸交于點C,連接BC,點D位拋物線的頂點,點P是第四象限的拋物線上的一個動點(不與點D重合).查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
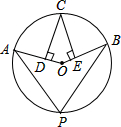 如圖,OA,OB分別為⊙O的半徑,若CD⊥OA,CE⊥OB,垂足分別為D,E,∠P=70°,則∠DCE的度數為( )
如圖,OA,OB分別為⊙O的半徑,若CD⊥OA,CE⊥OB,垂足分別為D,E,∠P=70°,則∠DCE的度數為( )| A. | 70° | B. | 60° | C. | 50° | D. | 40° |
查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
| A. | 3.5 | B. | 5.5 | C. | 7 | D. | 10 |
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
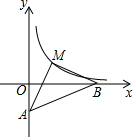 如圖,直線y=$\frac{1}{5}$x-1與x軸、y軸分別相交于B、A,點M為雙曲線y=$\frac{k}{x}$(x>0)上一點,若△AMB是以AB為底的等腰直角三角形,求S△MAB及k的值.
如圖,直線y=$\frac{1}{5}$x-1與x軸、y軸分別相交于B、A,點M為雙曲線y=$\frac{k}{x}$(x>0)上一點,若△AMB是以AB為底的等腰直角三角形,求S△MAB及k的值.查看答案和解析>>
科目:初中數學 來源: 題型:填空題
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
 如圖,四邊形ADBC中,∠D、∠C為直角,G、I分別是△ABC、△ABD的內心,延長AG、BG、AI、BI交四邊于Q、E、P、F,如果四邊形GAIB的面積為17,求六邊形EAFPBQ的面積.
如圖,四邊形ADBC中,∠D、∠C為直角,G、I分別是△ABC、△ABD的內心,延長AG、BG、AI、BI交四邊于Q、E、P、F,如果四邊形GAIB的面積為17,求六邊形EAFPBQ的面積.查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com