
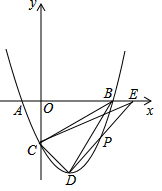
 如圖,在平面直角坐標系中,二次函數y=x2-2x-3的圖象與x軸交于A,B兩點,與y軸交于點C,連接BC,點D位拋物線的頂點,點P是第四象限的拋物線上的一個動點(不與點D重合).
如圖,在平面直角坐標系中,二次函數y=x2-2x-3的圖象與x軸交于A,B兩點,與y軸交于點C,連接BC,點D位拋物線的頂點,點P是第四象限的拋物線上的一個動點(不與點D重合).分析 (1)由拋物線已知,則可求三角形OBC的各個頂點,易知三角形形狀及內角.
(2)因為拋物線已固定,則S四邊形OCDB固定,對于坐標系中的不規則圖形常用分割求和、填補求差等方法求面積,本圖形過頂點作x軸的垂線及可將其分為直角梯形及直角三角形,面積易得.由此可得E點坐標,進而可求ED直線方程,與拋物線解析式聯立求解即得P點坐標.
解答 解:(1)∵y=x2-2x-3=(x-3)(x+1),
∴由題意得,A(-1,0),B(3,0),C(0,-3),D(1,-4).
在Rt△OBC中,
∵OC=OB=3,
∴△OBC為等腰直角三角形,
∴∠OBC=45°.
(2)如圖1,過點D作DH⊥x軸于H,
此時S四邊形OCDB=S梯形OCDH+S△HBD,
∵OH=1,OC=3,HD=4,HB=2,
∴S梯形OCDH=$\frac{1}{2}$•(OC+HD)•OH=$\frac{7}{2}$,
S△HBD=$\frac{1}{2}$•HD•HB=4,
∴S四邊形OCDB=$\frac{15}{2}$.
∴S△OCE=S四邊形OCDB=$\frac{15}{2}$=$\frac{1}{2}$•OC•OE,
∴OE=5,
∴E(5,0).
設lDE:y=kx+b,
∵D(1,-4),E(5,0),
∴$\left\{\begin{array}{l}{k+b=-4}\\{5k+b=0}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{k=1}\\{b=-5}\end{array}\right.$,
∴lDE:y=x-5.
∵DE交拋物線于P,設P(x,y),
∴x2-2x-3=x-5,
解得 x=2 或x=1(D點,舍去),
∴xP=2,代入lDE:y=x-5,
∴P(2,-3).
點評 本題考查了拋物線與x軸的交點,熟練掌握待定系數法求直線解析式、直角三角形性質及割補法求四邊形的面積、直線和拋物線交點問題是解題的關鍵.


 浙江名校名師金卷系列答案
浙江名校名師金卷系列答案科目:初中數學 來源: 題型:選擇題
 如圖,在△ABC中,∠ACB=90°,AC=BC=1,E、F為線段AB上兩動點,且∠ECF=45°,過點E、F分別作BC、AC的垂線相交于點M,垂足分別為H、G.現有以下結論:①AB=$\sqrt{2}$;②當點E與點B重合時,MH=$\frac{1}{2}$;③AF+BE=EF;④MG•MH=$\frac{1}{2}$,其中正確結論的個數是( )
如圖,在△ABC中,∠ACB=90°,AC=BC=1,E、F為線段AB上兩動點,且∠ECF=45°,過點E、F分別作BC、AC的垂線相交于點M,垂足分別為H、G.現有以下結論:①AB=$\sqrt{2}$;②當點E與點B重合時,MH=$\frac{1}{2}$;③AF+BE=EF;④MG•MH=$\frac{1}{2}$,其中正確結論的個數是( )| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
| A. | 第一天硬化的多 | B. | 第二天硬化的多 | C. | 兩天硬化一樣多 | D. | 無法確定 |
查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
| A. | (x-6)2=34 | B. | (x+6)2=34 | C. | (x-3)2=7 | D. | (x-3)2=11 |
查看答案和解析>>
科目:初中數學 來源: 題型:解答題

查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com