
 如圖,在△ABC中,∠ACB=90°,AC=BC=1,E、F為線段AB上兩動點,且∠ECF=45°,過點E、F分別作BC、AC的垂線相交于點M,垂足分別為H、G.現有以下結論:①AB=$\sqrt{2}$;②當點E與點B重合時,MH=$\frac{1}{2}$;③AF+BE=EF;④MG•MH=$\frac{1}{2}$,其中正確結論的個數是( )
如圖,在△ABC中,∠ACB=90°,AC=BC=1,E、F為線段AB上兩動點,且∠ECF=45°,過點E、F分別作BC、AC的垂線相交于點M,垂足分別為H、G.現有以下結論:①AB=$\sqrt{2}$;②當點E與點B重合時,MH=$\frac{1}{2}$;③AF+BE=EF;④MG•MH=$\frac{1}{2}$,其中正確結論的個數是( )| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
分析 ①由題意知,△ABC是等腰直角三角形,根據等腰直角三角形即可作出判斷;
②如圖1,當點E與點B重合時,點H與點B重合,可得MG∥BC,四邊形MGCB是矩形,進一步得到FG是△ACB的中位線,從而作出判斷;
③如圖2所示,SAS可證△ECF≌△ECD,根據全等三角形的性質和勾股定理即可作出判斷;
④根據AA可證△ACE∽△BFC,根據相似三角形的性質可得AF•BF=AC•BC=1,由題意知四邊形CHMG是矩形,再根據平行線的性質和等量代換得到MG•MH=$\frac{\sqrt{2}}{2}$AE×$\frac{\sqrt{2}}{2}$BF=$\frac{1}{2}$AE•BF=$\frac{1}{2}$AC•BC=$\frac{1}{2}$,依此即可作出判斷.
解答 解:①由題意知,△ABC是等腰直角三角形,
∴AB=$\sqrt{A{C}^{2}+B{C}^{2}}$=$\sqrt{2}$,故①正確;
②如圖1,當點E與點B重合時,點H與點B重合,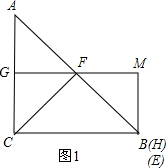
∴MB⊥BC,∠MBC=90°,
∵MG⊥AC,
∴∠MGC=90°=∠C=∠MBC,
∴MG∥BC,四邊形MGCB是矩形,
∴MH=MB=CG,
∵∠FCE=45°=∠ABC,∠A=∠ACF=45°,
∴CF=AF=BF,
∴FG是△ACB的中位線,
∴GC=$\frac{1}{2}$AC=MH,故②正確;
③如圖2所示,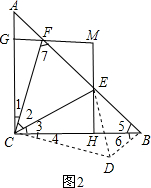
∵AC=BC,∠ACB=90°,
∴∠A=∠5=45°.
將△ACF順時針旋轉90°至△BCD,
則CF=CD,∠1=∠4,∠A=∠6=45°;BD=AF;
∵∠2=45°,
∴∠1+∠3=∠3+∠4=45°,
∴∠DCE=∠2.
在△ECF和△ECD中,
$\left\{\begin{array}{l}{CF=CD}\\{∠2=∠DCE}\\{CE=CE}\end{array}\right.$,
∴△ECF≌△ECD(SAS),
∴EF=DE.
∵∠5=45°,
∴∠DBE=90°,
∴DE2=BD2+BE2,即EF2=AF2+BE2,故③錯誤;
④∵∠7=∠1+∠A=∠1+45°=∠1+∠2=∠ACE,
∵∠A=∠5=45°,
∴△ACE∽△BFC,
∴$\frac{AE}{BC}$=$\frac{AC}{BF}$,
∴AE•BF=AC•BC=1,
由題意知四邊形CHMG是矩形,
∴MG∥BC,MH=CG,
MG=CH,MH∥AC,
∴$\frac{CH}{BC}$=$\frac{AE}{AB}$;$\frac{CG}{AC}$=$\frac{BF}{AB}$,
即$\frac{MG}{1}$=$\frac{AE}{\sqrt{2}}$;$\frac{MH}{1}$=$\frac{BF}{\sqrt{2}}$,
∴MG=$\frac{\sqrt{2}}{2}$AE;MH=$\frac{\sqrt{2}}{2}$BF,
∴MG•MH=$\frac{\sqrt{2}}{2}$AE×$\frac{\sqrt{2}}{2}$BF=$\frac{1}{2}$AE•BF=$\frac{1}{2}$AC•BC=$\frac{1}{2}$,故④正確;
故選:C.
點評 此題考查了三角形綜合題,涉及的知識點有:等腰直角三角形的判定和性質,平行線的判定和性質,矩形的判定和性質,三角形中位線的性質,全等三角形的判定和性質,勾股定理,相似三角形的判定和性質,綜合性較強,有一定的難度.


 智趣寒假作業云南科技出版社系列答案
智趣寒假作業云南科技出版社系列答案科目:初中數學 來源: 題型:解答題
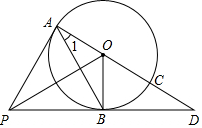 如圖,PA、PB是⊙O的切線,A、B為切點,AC是⊙O的直徑,AC、PB的延長線相交于點D.
如圖,PA、PB是⊙O的切線,A、B為切點,AC是⊙O的直徑,AC、PB的延長線相交于點D.查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
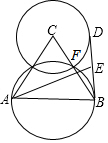 如圖,已知等邊△ABC的邊長為8,以AB為直徑的圓交BC于點F.以C為圓心,CF長為半徑作圖,D是⊙C上一動點,E為BD的中點,當AE最大時,BD的長為( )
如圖,已知等邊△ABC的邊長為8,以AB為直徑的圓交BC于點F.以C為圓心,CF長為半徑作圖,D是⊙C上一動點,E為BD的中點,當AE最大時,BD的長為( )| A. | $4\sqrt{3}$ | B. | $4\sqrt{5}$ | C. | $4\sqrt{3}+2$ | D. | 12 |
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
 鎮江某中學教師每天乘坐公交車上班.如圖是該教師坐在公交車上透過前面車輛的后窗玻璃拍攝到的該車的車號.若212路公交車途徑鎮江十中,215路途徑姚橋中學,512路途徑大港中學,515路途徑京口中學,那么該教師的工作地點是( )
鎮江某中學教師每天乘坐公交車上班.如圖是該教師坐在公交車上透過前面車輛的后窗玻璃拍攝到的該車的車號.若212路公交車途徑鎮江十中,215路途徑姚橋中學,512路途徑大港中學,515路途徑京口中學,那么該教師的工作地點是( )| A. | 鎮江十中 | B. | 姚橋中學 | C. | 大港中學 | D. | 京口中學 |
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
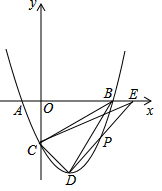 如圖,在平面直角坐標系中,二次函數y=x2-2x-3的圖象與x軸交于A,B兩點,與y軸交于點C,連接BC,點D位拋物線的頂點,點P是第四象限的拋物線上的一個動點(不與點D重合).
如圖,在平面直角坐標系中,二次函數y=x2-2x-3的圖象與x軸交于A,B兩點,與y軸交于點C,連接BC,點D位拋物線的頂點,點P是第四象限的拋物線上的一個動點(不與點D重合).查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com