
 如圖,四邊形ADBC中,∠D、∠C為直角,G、I分別是△ABC、△ABD的內(nèi)心,延長AG、BG、AI、BI交四邊于Q、E、P、F,如果四邊形GAIB的面積為17,求六邊形EAFPBQ的面積.
如圖,四邊形ADBC中,∠D、∠C為直角,G、I分別是△ABC、△ABD的內(nèi)心,延長AG、BG、AI、BI交四邊于Q、E、P、F,如果四邊形GAIB的面積為17,求六邊形EAFPBQ的面積. 分析 如圖,在線段AB上分別截取AM=AE,BN=BQ,連接GM、GN,作QH⊥BE于H,ND⊥GM于D.只要證明六邊形EAFPBQ的面積=2•四邊形GAIB的面積即可解決問題.
解答 解:如圖,在線段AB上分別截取AM=AE,BN=BQ,連接GM、GN,作QH⊥BE于H,ND⊥GM于D.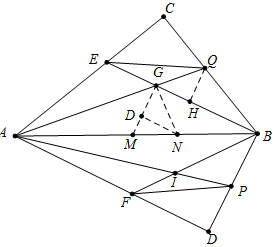
在△AGE和△AGM中,
$\left\{\begin{array}{l}{AG=AG}\\{∠GAE=∠GAM}\\{AE=AM}\end{array}\right.$,
∴△GAE≌△GAM,
∴GE=GM,∠AGE=∠AGM,
同理可證△GBQ≌△GBN,可得GQ=GN,
∵∠C=90°,∠GAB=$\frac{1}{2}$∠CAB,∠GBA=$\frac{1}{2}$∠CBA,
∴∠QCB=∠AGE=∠GAB+∠GBA=45°,
∴∠EGM=∠QGN=90°,
∴∠EGQ+∠MGN=180°,∵∠EGQ+∠QGB=180°,
∴∠QGH=∠MGN,
∵S△EGQ=$\frac{1}{2}$•EG•QG•sin∠QGH,S△MNG=$\frac{1}{2}$•GM•GN•sin∠MGN,
∴S△EGQ=S△MGN,S△AMG=S△AGE,S△GBN=S△GBQ,
∴S△ABG=S△AEG+S△EQG+S△GBQ,
同理可證S△ABI=S△AIF+S△IPF+S△BIP,
∴六邊形EAFPBQ的面積=2•四邊形GAIB的面積=34.
點評 本題考查三角形的內(nèi)心,三角形的面積,四邊形的面積,全等三角形的判定和性質(zhì)等知識,解題的關(guān)鍵是學會添加常用輔助線構(gòu)造全等三角形解決問題嗎,屬于中考壓軸題.


 名校課堂系列答案
名校課堂系列答案科目:初中數(shù)學 來源: 題型:解答題

查看答案和解析>>
科目:初中數(shù)學 來源: 題型:解答題
查看答案和解析>>
科目:初中數(shù)學 來源: 題型:解答題
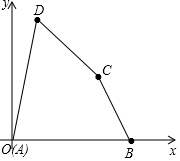 如圖,已知在平面直角坐標系中,四邊形各頂點的坐標分別為A(0,0),B(9,0),C(7,4),D(2,8),求四邊形ABCD的面積.
如圖,已知在平面直角坐標系中,四邊形各頂點的坐標分別為A(0,0),B(9,0),C(7,4),D(2,8),求四邊形ABCD的面積.查看答案和解析>>
科目:初中數(shù)學 來源: 題型:解答題
 如圖,BF,BE分別是∠ABC及其鄰補角的平分線,AE⊥BE于點E,AF⊥BF于點F,四邊形AEBF是矩形嗎?請證明你的結(jié)論.
如圖,BF,BE分別是∠ABC及其鄰補角的平分線,AE⊥BE于點E,AF⊥BF于點F,四邊形AEBF是矩形嗎?請證明你的結(jié)論.查看答案和解析>>
科目:初中數(shù)學 來源: 題型:解答題
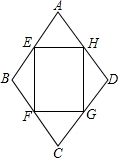 如圖,四邊形ABCD是一個菱形綠草地,其周長為40$\sqrt{2}$m,∠ABC=120°,在其內(nèi)部有一個矩形花壇EFGH,其四個頂點恰好在菱形ABCD各邊中點,現(xiàn)準備在花壇中種植茉莉花,其單價為30元/2,則需投資資金多少元?($\sqrt{3}$取1.732)
如圖,四邊形ABCD是一個菱形綠草地,其周長為40$\sqrt{2}$m,∠ABC=120°,在其內(nèi)部有一個矩形花壇EFGH,其四個頂點恰好在菱形ABCD各邊中點,現(xiàn)準備在花壇中種植茉莉花,其單價為30元/2,則需投資資金多少元?($\sqrt{3}$取1.732)查看答案和解析>>
科目:初中數(shù)學 來源: 題型:填空題
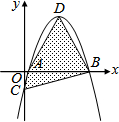 如圖,坐標平面上,二次函數(shù)y=-x2+4x-k的圖形與x軸交于A,B兩點,與y軸交于C點,其頂點為D,且k>0,若△ABC與△ABD的面積比為1:4,則k的值為$\frac{4}{5}$.
如圖,坐標平面上,二次函數(shù)y=-x2+4x-k的圖形與x軸交于A,B兩點,與y軸交于C點,其頂點為D,且k>0,若△ABC與△ABD的面積比為1:4,則k的值為$\frac{4}{5}$.查看答案和解析>>
科目:初中數(shù)學 來源: 題型:選擇題
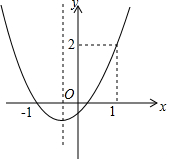 已知拋物線y=ax2+bx+c的圖象如圖所示,則下列結(jié)論:
已知拋物線y=ax2+bx+c的圖象如圖所示,則下列結(jié)論:| A. | ①② | B. | ②③ | C. | ③④ | D. | ②④ |
查看答案和解析>>
科目:初中數(shù)學 來源: 題型:選擇題
 如圖,A、B、C是⊙O上的三點,∠B=75°,則∠AOC的度數(shù)是( )
如圖,A、B、C是⊙O上的三點,∠B=75°,則∠AOC的度數(shù)是( )| A. | 120° | B. | 130° | C. | 140° | D. | 150° |
查看答案和解析>>
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com