
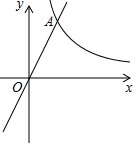
 已知:如圖,在平面直角坐標系xOy中,反比例函數y=$\frac{8}{x}$的圖象與正比例函數y=kx(k≠0)的圖象相交于橫坐標為2的點A,平移直線OA,使它經過點B(3,0).
已知:如圖,在平面直角坐標系xOy中,反比例函數y=$\frac{8}{x}$的圖象與正比例函數y=kx(k≠0)的圖象相交于橫坐標為2的點A,平移直線OA,使它經過點B(3,0).分析 (1)將x=2代入反比例函數的解析式求出點A的坐標,然后將A的坐標代入直線OA的解析式中求出k的值,由于平移,所以直線OB與直線OA的一次項系數必相等,最后將B(3,0)代入即可求出平移后直線的解析式.
(2)聯立直線與雙曲線的解析式即可求出交點坐標.
解答 解:(1)當x=2時,y=$\frac{8}{2}$=4,
∴A的坐標為(2,4)
將A(2,4)代入y=kx,
∴4=2k
∴k=2,
∴直線OA的表達式y=2x
設平移后的直線表達式為y=2x+b
將B(3,0)代入y=2x+b
∴0=2×3+b,解得b=-6
∴平移后的直線表達式為:y=2x-6
(2)聯立$\left\{\begin{array}{l}{y=\frac{8}{x}}\\{y=2x-6}\end{array}\right.$
解得:$\left\{\begin{array}{l}{x=4}\\{y=2}\end{array}\right.$或$\left\{\begin{array}{l}{x=-1}\\{y=-8}\end{array}\right.$
∴OA平移后所得直線與雙曲線的交點坐標為(4,2),(-1,-8)
點評 本題考查反比例函數的綜合問題,解題的關鍵是求出直線OA與平移后直線的解析式,本題屬于中等題型.


 培優三好生系列答案
培優三好生系列答案 優化作業上海科技文獻出版社系列答案
優化作業上海科技文獻出版社系列答案科目:初中數學 來源: 題型:填空題
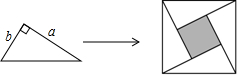 如圖所示,用四個直角邊分別為a、b(a>b)的直角三角形拼成一個中間留有空隙(即圖中陰影部分的小正方形)的大正方形,空隙的面積為10,則a-b的值為$\sqrt{10}$.
如圖所示,用四個直角邊分別為a、b(a>b)的直角三角形拼成一個中間留有空隙(即圖中陰影部分的小正方形)的大正方形,空隙的面積為10,則a-b的值為$\sqrt{10}$.查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
 如圖,已知一次函數y=x-2與反比例函數y=$\frac{3}{x}$的圖象交于A、B兩點.
如圖,已知一次函數y=x-2與反比例函數y=$\frac{3}{x}$的圖象交于A、B兩點.查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
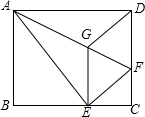 如圖,將矩形ABCD沿AF折疊,使點D落在BC邊的點E處,過點E作EG∥CD交AF于點G,連接DG.給出以下結論:①DG=DF;②四邊形EFDG是菱形;③EG2=$\frac{1}{2}$GF×AF;④當AG=6,EG=2$\sqrt{5}$時,BE的長為$\frac{12}{5}$$\sqrt{5}$,其中正確的結論個數是( )
如圖,將矩形ABCD沿AF折疊,使點D落在BC邊的點E處,過點E作EG∥CD交AF于點G,連接DG.給出以下結論:①DG=DF;②四邊形EFDG是菱形;③EG2=$\frac{1}{2}$GF×AF;④當AG=6,EG=2$\sqrt{5}$時,BE的長為$\frac{12}{5}$$\sqrt{5}$,其中正確的結論個數是( )| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
 如圖所示,表示甲騎電動車與乙駕駛汽車勻速行駛120km的過程中行駛的路程y與經過的時間x之間的函數圖象,請根據圖象解答下列問題:
如圖所示,表示甲騎電動車與乙駕駛汽車勻速行駛120km的過程中行駛的路程y與經過的時間x之間的函數圖象,請根據圖象解答下列問題:查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com