
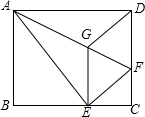
 如圖,將矩形ABCD沿AF折疊,使點D落在BC邊的點E處,過點E作EG∥CD交AF于點G,連接DG.給出以下結論:①DG=DF;②四邊形EFDG是菱形;③EG2=$\frac{1}{2}$GF×AF;④當AG=6,EG=2$\sqrt{5}$時,BE的長為$\frac{12}{5}$$\sqrt{5}$,其中正確的結論個數是( )
如圖,將矩形ABCD沿AF折疊,使點D落在BC邊的點E處,過點E作EG∥CD交AF于點G,連接DG.給出以下結論:①DG=DF;②四邊形EFDG是菱形;③EG2=$\frac{1}{2}$GF×AF;④當AG=6,EG=2$\sqrt{5}$時,BE的長為$\frac{12}{5}$$\sqrt{5}$,其中正確的結論個數是( )| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
分析 先依據翻折的性質和平行線的性質證明∠DGF=∠DFG,從而得到GD=DF,接下來依據翻折的性質可證明DG=GE=DF=EF,連接DE,交AF于點O.由菱形的性質可知GF⊥DE,OG=OF=$\frac{1}{2}$GF,接下來,證明△DOF∽△ADF,由相似三角形的性質可證明DF2=FO•AF,于是可得到GE、AF、FG的數量關系,過點G作GH⊥DC,垂足為H.利用(2)的結論可求得FG=4,然后再△ADF中依據勾股定理可求得AD的長,然后再證明△FGH∽△FAD,利用相似三角形的性質可求得GH的長,最后依據BE=AD-GH求解即可.
解答 解:∵GE∥DF,
∴∠EGF=∠DFG.
∵由翻折的性質可知:GD=GE,DF=EF,∠DGF=∠EGF,
∴∠DGF=∠DFG.
∴GD=DF.故①正確;
∴DG=GE=DF=EF.
∴四邊形EFDG為菱形,故②正確;
如圖1所示:連接DE,交AF于點O.
∵四邊形EFDG為菱形,
∴GF⊥DE,OG=OF=$\frac{1}{2}$GF.
∵∠DOF=∠ADF=90°,∠OFD=∠DFA,
∴△DOF∽△ADF.
∴$\frac{DF}{AF}$=$\frac{OF}{DF}$,即DF2=FO•AF.
∵FO=$\frac{1}{2}$GF,DF=EG,
∴EG2=$\frac{1}{2}$GF•AF.故③正確;
如圖2所示:過點G作GH⊥DC,垂足為H.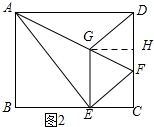
∵EG2=$\frac{1}{2}$GF•AF,AG=6,EG=2$\sqrt{5}$,
∴20=$\frac{1}{2}$FG(FG+6),整理得:FG2+6FG-40=0.
解得:FG=4,FG=-10(舍去).
∵DF=GE=2$\sqrt{5}$,AF=10,
∴AD=$\sqrt{A{F}^{2}-D{F}^{2}}$=4$\sqrt{5}$.
∵GH⊥DC,AD⊥DC,
∴GH∥AD.
∴△FGH∽△FAD.
∴$\frac{GH}{AD}$=$\frac{FG}{AF}$,即$\frac{GH}{4\sqrt{5}}$=$\frac{4}{10}$,
∴GH=$\frac{8\sqrt{5}}{5}$,
∴BE=AD-GH=4$\sqrt{5}$-$\frac{8\sqrt{5}}{5}$=$\frac{12\sqrt{5}}{5}$.故④正確.
故選D.
點評 本題主要考查的是四邊形與三角形的綜合應用,解答本題主要應用了矩形的性質、菱形的判定和性質、相似三角形的性質和判定、勾股定理的應用,利用相似三角形的性質得到DF2=FO•AF是解題答問題②的關鍵,依據相似三角形的性質求得GH的長是解答問題④的關鍵.


科目:初中數學 來源: 題型:解答題
 如圖,已知AB是⊙O的直徑,C是⊙O上一點,∠BAC的平分線交⊙O于點D,交⊙O的切線BE于點E,過點D作DF⊥AC,交AC的延長線于點F.
如圖,已知AB是⊙O的直徑,C是⊙O上一點,∠BAC的平分線交⊙O于點D,交⊙O的切線BE于點E,過點D作DF⊥AC,交AC的延長線于點F.查看答案和解析>>
科目:初中數學 來源: 題型:解答題
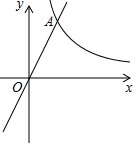 已知:如圖,在平面直角坐標系xOy中,反比例函數y=$\frac{8}{x}$的圖象與正比例函數y=kx(k≠0)的圖象相交于橫坐標為2的點A,平移直線OA,使它經過點B(3,0).
已知:如圖,在平面直角坐標系xOy中,反比例函數y=$\frac{8}{x}$的圖象與正比例函數y=kx(k≠0)的圖象相交于橫坐標為2的點A,平移直線OA,使它經過點B(3,0).查看答案和解析>>
科目:初中數學 來源: 題型:解答題

查看答案和解析>>
科目:初中數學 來源: 題型:填空題

查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
科目:初中數學 來源: 題型:解答題

查看答案和解析>>
科目:初中數學 來源: 題型:解答題
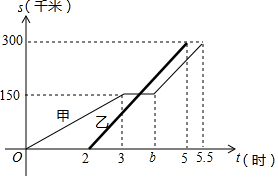 甲、乙兩輛汽車沿同一路線從A地前往B地,甲以a千米/時的速度勻速行駛,途中出現故障后停車維修,修好后以2a千米/時的速度繼續行駛;乙在甲出發2小時后勻速前往B地,設甲、乙兩車與A地的路程為s(千米),甲車離開A地的時間為t(時),s與t之間的函數圖象如圖所示.
甲、乙兩輛汽車沿同一路線從A地前往B地,甲以a千米/時的速度勻速行駛,途中出現故障后停車維修,修好后以2a千米/時的速度繼續行駛;乙在甲出發2小時后勻速前往B地,設甲、乙兩車與A地的路程為s(千米),甲車離開A地的時間為t(時),s與t之間的函數圖象如圖所示.查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com