
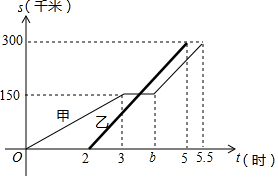
 甲、乙兩輛汽車沿同一路線從A地前往B地,甲以a千米/時的速度勻速行駛,途中出現(xiàn)故障后停車維修,修好后以2a千米/時的速度繼續(xù)行駛;乙在甲出發(fā)2小時后勻速前往B地,設(shè)甲、乙兩車與A地的路程為s(千米),甲車離開A地的時間為t(時),s與t之間的函數(shù)圖象如圖所示.
甲、乙兩輛汽車沿同一路線從A地前往B地,甲以a千米/時的速度勻速行駛,途中出現(xiàn)故障后停車維修,修好后以2a千米/時的速度繼續(xù)行駛;乙在甲出發(fā)2小時后勻速前往B地,設(shè)甲、乙兩車與A地的路程為s(千米),甲車離開A地的時間為t(時),s與t之間的函數(shù)圖象如圖所示.分析 (1)根據(jù)速度=路程÷時間即可求出a值,再根據(jù)時間=路程÷速度算出b到5.5之間的時間段,由此即可求出b值;
(2)觀察圖形找出兩點的坐標(biāo),利用待定系數(shù)法即可求出s乙關(guān)于t的函數(shù)關(guān)系式,令s乙=150即可求出兩車相遇的時間;
(3)分0≤t≤3、3≤t≤4和4≤t≤5.5三段求出s甲關(guān)于t的函數(shù)關(guān)系式,二者做差令其絕對值等于60即可得出關(guān)于t的函數(shù)絕對值符號的一元一次方程,解之即可求出t值,再求出0≤t≤2時,s甲=50t=60中t的值.綜上即可得出結(jié)論.
解答 解:(1)a=$\frac{150}{3}$=50,
b=5.5-$\frac{300-150}{2×50}$=4.
(2)設(shè)乙車與A地的路程s與甲車離開A地的時間t之間的函數(shù)關(guān)系式為s乙=kt+m,
將(2,0)、(5,300)代入s=kt+m,
$\left\{\begin{array}{l}{0=2k+m}\\{300=5k+m}\end{array}\right.$,解得:$\left\{\begin{array}{l}{k=100}\\{m=-200}\end{array}\right.$,
∴s乙=100t-200(2≤t≤5).
當(dāng)s乙=100t-200=150時,t=3.5.
答:兩車在途中相遇時t的值為3.5.
(3)當(dāng)0≤t≤3時,s甲=50t;
當(dāng)3≤t≤4時,s甲=150;
當(dāng)4≤t≤5.5時,s甲=150+2×50(t-4)=100t-250.
∴s甲=$\left\{\begin{array}{l}{50t(0≤t≤3)}\\{150(3≤t≤4)}\\{100t-250(4≤t≤5.5)}\end{array}\right.$.
令|s甲-s乙|=60,即|50t-100t+200|=60,|150-100t+200|=60或|100t-250-100t+200|=60,
解得:t1=$\frac{14}{5}$,t2=$\frac{26}{5}$(舍去),t3=$\frac{29}{10}$(舍去),t4=$\frac{41}{10}$(舍去);
當(dāng)0≤t≤2時,令s甲=50t=60,解得:t=$\frac{6}{5}$.
綜上所述:當(dāng)兩車相距60千米時,t=$\frac{6}{5}$或$\frac{14}{5}$.
故答案為:$\frac{6}{5}$或$\frac{14}{5}$.
點評 本題考查了一次函數(shù)的應(yīng)用、待定系數(shù)法求函數(shù)解析式以及解含絕對值符號的一元一次方程,解題的關(guān)鍵是:(1)根據(jù)數(shù)量關(guān)系列式計算;(2)根據(jù)點的坐標(biāo)利用待定系數(shù)法求出函數(shù)關(guān)系式;(3)根據(jù)數(shù)量關(guān)系求出s甲關(guān)于t的函數(shù)關(guān)系式.


科目:初中數(shù)學(xué) 來源: 題型:選擇題
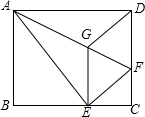 如圖,將矩形ABCD沿AF折疊,使點D落在BC邊的點E處,過點E作EG∥CD交AF于點G,連接DG.給出以下結(jié)論:①DG=DF;②四邊形EFDG是菱形;③EG2=$\frac{1}{2}$GF×AF;④當(dāng)AG=6,EG=2$\sqrt{5}$時,BE的長為$\frac{12}{5}$$\sqrt{5}$,其中正確的結(jié)論個數(shù)是( )
如圖,將矩形ABCD沿AF折疊,使點D落在BC邊的點E處,過點E作EG∥CD交AF于點G,連接DG.給出以下結(jié)論:①DG=DF;②四邊形EFDG是菱形;③EG2=$\frac{1}{2}$GF×AF;④當(dāng)AG=6,EG=2$\sqrt{5}$時,BE的長為$\frac{12}{5}$$\sqrt{5}$,其中正確的結(jié)論個數(shù)是( )| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:解答題
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:解答題
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:解答題

查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:選擇題
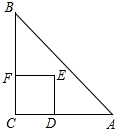 如圖,Rt△ABC中,∠C=90°,AC=BC=2,正方形CDEF的頂點D、F分別在AC、BC上,C、D兩點不重合,設(shè)CD的長度為x,Rt△ABC與正方形CDEF重疊部分的面積為y,則下列中能表示y與x之間的關(guān)系的是( )
如圖,Rt△ABC中,∠C=90°,AC=BC=2,正方形CDEF的頂點D、F分別在AC、BC上,C、D兩點不重合,設(shè)CD的長度為x,Rt△ABC與正方形CDEF重疊部分的面積為y,則下列中能表示y與x之間的關(guān)系的是( )| A. |  | B. | 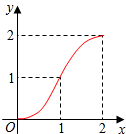 | C. | 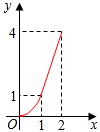 | D. | 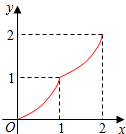 |
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:解答題
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:解答題
查看答案和解析>>
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com