
分析 (1)把k代入拋物線解析式,然后利用配方法可確定拋物線的頂點坐標;
(2)計算判別式的值,然后判別式的意義進行證明.
解答 (1)解:把k=$\frac{1}{2}$代入y=x2-(2k+1)x+k2+k(k>0)得y=x2-2x+$\frac{3}{4}$,
因為y=(x-1)2-$\frac{1}{4}$
所以拋物線的頂點坐標為(1,-$\frac{1}{4}$);
(2)證明:△=(2k+1)2-4(k2+k)=1>0,
所以關于x的一元二次方程x2-(2k+1)x+k2+k=0有兩個不相等的實數根.
點評 本題考查了拋物線與x軸的交點:對于二次函數y=ax2+bx+c(a,b,c是常數,a≠0),△=b2-4ac決定拋物線與x軸的交點個數:△=b2-4ac>0時,拋物線與x軸有2個交點;△=b2-4ac=0時,拋物線與x軸有1個交點;△=b2-4ac<0時,拋物線與x軸沒有交點.


科目:初中數學 來源: 題型:解答題
 如圖,已知AB是⊙O的直徑,C是⊙O上一點,∠BAC的平分線交⊙O于點D,交⊙O的切線BE于點E,過點D作DF⊥AC,交AC的延長線于點F.
如圖,已知AB是⊙O的直徑,C是⊙O上一點,∠BAC的平分線交⊙O于點D,交⊙O的切線BE于點E,過點D作DF⊥AC,交AC的延長線于點F.查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
科目:初中數學 來源: 題型:解答題

查看答案和解析>>
科目:初中數學 來源: 題型:填空題
 如圖所示,某人從甲地出發,騎摩托車去乙地,途中因車出現故障而停車修理,到達乙地時正好用了2小時,已知摩托車行駛的路程s(千米)與行駛的時間t(時)之間的函數關系由下面的圖象OBCD給出,若這輛摩托車平均每行駛100千米的耗油量為2升,則從甲地到乙地,這輛摩托車耗油量為0.9升,車修好后,摩托車的速度為30千米/小時.
如圖所示,某人從甲地出發,騎摩托車去乙地,途中因車出現故障而停車修理,到達乙地時正好用了2小時,已知摩托車行駛的路程s(千米)與行駛的時間t(時)之間的函數關系由下面的圖象OBCD給出,若這輛摩托車平均每行駛100千米的耗油量為2升,則從甲地到乙地,這輛摩托車耗油量為0.9升,車修好后,摩托車的速度為30千米/小時.查看答案和解析>>
科目:初中數學 來源: 題型:解答題
 如圖,方格紙中的每個小方格都是邊長為1的正方形,我們把以格點間連線為邊的三角形稱為“格點三角形”,圖中的△ABC就是格點三角形,建立如圖所示的平面直角坐標系,點C的坐標為(0,-1).
如圖,方格紙中的每個小方格都是邊長為1的正方形,我們把以格點間連線為邊的三角形稱為“格點三角形”,圖中的△ABC就是格點三角形,建立如圖所示的平面直角坐標系,點C的坐標為(0,-1).查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
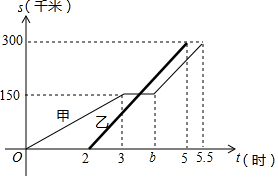 甲、乙兩輛汽車沿同一路線從A地前往B地,甲以a千米/時的速度勻速行駛,途中出現故障后停車維修,修好后以2a千米/時的速度繼續行駛;乙在甲出發2小時后勻速前往B地,設甲、乙兩車與A地的路程為s(千米),甲車離開A地的時間為t(時),s與t之間的函數圖象如圖所示.
甲、乙兩輛汽車沿同一路線從A地前往B地,甲以a千米/時的速度勻速行駛,途中出現故障后停車維修,修好后以2a千米/時的速度繼續行駛;乙在甲出發2小時后勻速前往B地,設甲、乙兩車與A地的路程為s(千米),甲車離開A地的時間為t(時),s與t之間的函數圖象如圖所示.查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com