
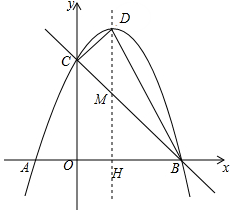
 如圖,已知拋物線y=-x2+bx+c軸交于A(-1,0)、B(3,0)兩點,與y軸交于點C,拋物線的對稱軸與拋物線交于點P,與直線BC相交于點M,連接PB.
如圖,已知拋物線y=-x2+bx+c軸交于A(-1,0)、B(3,0)兩點,與y軸交于點C,拋物線的對稱軸與拋物線交于點P,與直線BC相交于點M,連接PB.分析 (1)由B、C兩點的坐標,利用待定系數法可求得拋物線的解析式;
(2)設D(t,-t2+2t+3),過點D作DH⊥x軸,根據S△BCD=S梯形OCDH+S△BDH-S△BOC構建二次函數,利用二次函數的性質即可解決問題.
(3)設直線m與y軸交于點N,交直線l于點G,由于∠AGP=∠GNC+∠GCN,所以當△AGB和△NGC相似時,必有∠AGB=∠CGB=90°,則可證得△AOC≌△NOB,可求得ON的長,可求出N點坐標,利用B、N兩的點坐標可求得直線m的解析式.
解答 解:(1)∵拋物線y=-x2+bx+c軸交于A(-1,0)、B(3,0)兩點,
則有$\left\{\begin{array}{l}{-1-b+c=0}\\{-9+3b+c=0}\end{array}\right.$解得$\left\{\begin{array}{l}{b=2}\\{c=3}\end{array}\right.$,
∴拋物線的解析式為y=-x2+2x+3.
(2)設D(t,-t2+2t+3),過點D作DH⊥x軸, ,
,
則S△BCD=S梯形OCDH+S△BDH-S△BOC
=$\frac{1}{2}$(-t2+2t+3+3)t+$\frac{1}{2}$(3-t)(-t2+2t+3)-$\frac{1}{2}$×3×
3=-$\frac{3}{2}$t2+$\frac{9}{2}$t=-$\frac{3}{2}$(t-$\frac{3}{2}$)2+$\frac{27}{8}$
∵-$\frac{3}{2}$<0,
∴當t=-$\frac{\frac{9}{2}}{2×(-\frac{3}{2})}$=$\frac{3}{2}$時,D點坐標是($\frac{3}{2}$,$\frac{15}{4}$),△BCD面積的最大值是$\frac{27}{8}$.
(3)①如圖,設直線m與y軸交于點N,交直線l于點G,由于∠AGP=∠GNC+∠GCN,所以當△AGB和△NGC相似時,必有∠AGB=∠CGB=90°,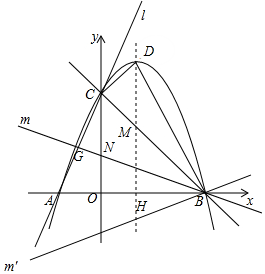
∵∠CNG=∠BNO,∠CGN=∠NOB=90°,
∴∠ACO=∠OBN,
在△AOC和△NOB中,
$\left\{\begin{array}{l}{∠ACO=∠OBN}\\{∠AOC=∠BON}\\{OC=OB}\end{array}\right.$,
∴△AOC≌△NOB,
∴ON=AO=1,
∴N(0,1),
設直線BG的解析式為y=kx+b,則有$\left\{\begin{array}{l}{b=1}\\{3k+b=0}\end{array}\right.$解得$\left\{\begin{array}{l}{k=-\frac{1}{3}}\\{b=1}\end{array}\right.$,
∴直線BG的解析式為y=-$\frac{1}{3}$x+1,
②當點Q在x軸上方時,此時直線m與①中的直線m關于x軸對稱,
∴解析式為y=$\frac{1}{3}$x+1;
綜上可知存在滿足條件的直線m,其解析式為y=$\frac{1}{3}$x-1或y=-$\frac{1}{3}$x+1.
點評 本題為二次函數的綜合應用,涉及知識點有待定系數法、二次函數的最值、相似三角形的判定、全等三角形的判定和性質等.在(2)中構建二次函數是解題的關鍵,在(3)中確定出滿足條件的直線m的位置是解題的關鍵.


科目:初中數學 來源: 題型:解答題
查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
| A. | 若x=y,則xm-5=ym-5 | B. | 若(a2+1)x=1,則x=$\frac{1}{{a}^{2}+1}$ | ||
| C. | 若x2=3x,則x=3 | D. | 若m=n,則am=an |
查看答案和解析>>
科目:初中數學 來源: 題型:解答題

查看答案和解析>>
科目:初中數學 來源: 題型:解答題
| 每回投球次數 | 30 | 60 | 90 | 150 | 200 | 300 | 400 | 500 |
| 每回進球次數 | 27 | 45 | 78 | 118 | 161 | 239 | 322 | 401 |
| 進球頻率 | 0.900 | 0.750 | 0.867 | 0.787 | 0.805 | 0.797 | 0.805 | 0.802 |
查看答案和解析>>
科目:初中數學 來源: 題型:填空題
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com