Question

7．如圖，直線l₁∥l₂，⊙O與l₁和l₂分別相切于點A和點B．點M和點N分別是l₁和l₂上的動點，MN沿l₁和l₂平移．⊙O的半徑為1，∠1=60°．有下列結論：①MN=$\frac{4\sqrt{3}}{3}$；②若MN與⊙O相切，則AM=$\sqrt{3}$；③若∠MON=90°，則MN與⊙O相切；④l₁和l₂的距離為2，其中正確的有（　　）

• A． 4個
• B． 3個
• C． 2個
• D． 1個．

Answer 1

分析 首先過點N作NC⊥AM于點C，直線l₁∥l₂，⊙O與l₁和l₂分別相切于點A和點B，⊙O的半徑為1，易求得MN=$\frac{CN}{sin60°}$=$\frac{4\sqrt{3}}{3}$，l₁和l₂的距離為2；若∠MON=90°，連接NO并延長交MA于點C，易證得CO=NO，繼而可得即O到MN的距離等于半徑，可證得MN與⊙O相切；由題意可求得若MN與⊙O相切，則AM=$\sqrt{3}$或$\frac{\sqrt{3}}{3}$．

解答 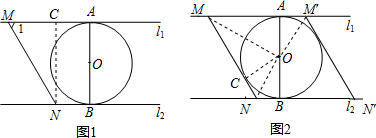解：如圖1，過點N作NC⊥AM于點C，
∵直線l₁∥l₂，⊙O與l₁和l₂分別相切于點A和點B，⊙O的半徑為1，
∴CN=AB=2，
∵∠1=60°，
∴MN=$\frac{CN}{sin60°}$=$\frac{4\sqrt{3}}{3}$，
故①與④正確；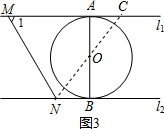
如圖3，
若∠MON=90°，連接NO并延長交MA于點C，則△AOC≌△BON，
故CO=NO，△MON≌△MOM′，故MN上的高為1，即O到MN的距離等于半徑．
故③正確；
如圖2，∵MN是切線，⊙O與l₁和l₂分別相切于點A和點B，
∴∠AMO=$\frac{1}{2}$∠1=30°，
∴AM=$\sqrt{3}$；
∵∠AM′O=60°，
∴AM′=$\frac{\sqrt{3}}{3}$，
∴若MN與⊙O相切，則AM=$\sqrt{3}$或$\frac{\sqrt{3}}{3}$；
故②錯誤．
故選B．

點評 此題考查了切線的判定與性質、全等三角形的判定與性質以及三角函數等知識．此題難度較大，注意掌握數形結合思想與分類討論思想的應用．