Question

12．如圖所示，在圓⊙O內有折線OAB，其中OA=8，AB=12，∠A=∠B=60°，則BC的長為（　　）

• A． 20
• B． 19
• C． 18
• D． 16

Answer 1

分析 延長AO交BC于D，根據∠A、∠B的度數易證得△ABD是等邊三角形，由此可求出OD、BD的長；過O作BC的垂線，設垂足為E；在Rt△ODE中，根據OD的長及∠ODE的度數易求得DE的長，進而可求出BE的長；由垂徑定理知BC=2BE，由此得解．

解答 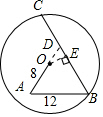解：延長AO交BC于D，作OE⊥BC于E；
∵∠A=∠B=60°，∴∠ADB=60°；
∴△ADB為等邊三角形；
∴BD=AD=AB=12；
∴OD=4，又∵∠ADB=60°，
∴DE=$\frac{1}{2}$OD=2；
∴BE=10；
∴BC=2BE=20．
故選A．

點評 此題主要考查了等邊三角形的判定和性質以及垂徑定理的應用，正確作出輔助線是關鍵．