
分析 (1)根據(jù)奇數(shù)與偶數(shù)的定義寫出即可;
(2)任意兩個整數(shù)的和與這兩個數(shù)的差是同時為奇數(shù)或同時為偶數(shù);
(3)分①設(shè)a=2m,b=2n,②設(shè)a=2m,b=2n+1,③設(shè)a=2m+1,b=2n,④設(shè)a=2m+1,b=2n+1四種情況討論可證明結(jié)論;
(4)由(3)的結(jié)論得出;
(5)應(yīng)用第(2)、(3)、(4)的結(jié)論完成.
解答 解:(1)用含有n的代數(shù)式表示任意一個偶數(shù)為2n,用含有n的代數(shù)式表示任意一個奇數(shù)為2n+1或2n-1(奇數(shù)的表達式寫出一個即可);
(2)任意兩個整數(shù)的和與這兩個數(shù)的差是同時為奇數(shù)或同時為偶數(shù);
(3)②設(shè)a=2m,b=2n+1,
則:a+b=2m+2n+1=2(m+n)+1a-b=2m-(2n+1)=2(m-n)-1,
此時a+b和a-b同時為奇數(shù);
③設(shè)a=2m+1,b=2n,
則:a+b=2m+1+2n=2(m+n)+1a-b=2m+1-2n=2(m-n)+1,
此時a+b和a-b同時為奇數(shù);
④設(shè)a=2m+1,b=2n+1,
則:a+b=2m+1+2n+1=2(m+n+1)a-b=(2m+1)-(2n+1)=2(m-n),
此時a+b和a-b同時為偶數(shù),
由此可見:a+b和a-b要么同時為奇數(shù),要么同時為偶數(shù),
即a+b和a-b的奇偶性相同;
(4)由(3)的結(jié)論:
-a+b=b-a與a+b=b+a奇偶性相同,
-a-b=-b-a與a-b=-b+a奇偶性相同,
因此-a+b、-a-b、a+b、a-b“同奇”或“同偶”;
(5)在2016個自然數(shù)1,2,3,…,2015,2016的每一個數(shù)的前面任意添加“+”或“-”,則其代數(shù)和一定是偶數(shù).
故答案為:2n,2n+1或2n-1;是;偶數(shù).
點評 本題主要考查了整式的加減,奇數(shù)與偶數(shù)的意義及推到偶數(shù)+偶數(shù)=偶數(shù),奇數(shù)+奇數(shù)=偶數(shù)的過程.


 名牌學校分層周周測系列答案
名牌學校分層周周測系列答案 黃岡海淀全程培優(yōu)測試卷系列答案
黃岡海淀全程培優(yōu)測試卷系列答案科目:初中數(shù)學 來源: 題型:填空題
查看答案和解析>>
科目:初中數(shù)學 來源: 題型:填空題
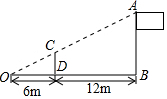 如圖,小明用長為2.5m的竹竿CD做測量工具,測量學校旗桿AB的高度,移動竹竿,使竹竿、旗桿的頂端的影子恰好落在地面的同一點O.此時,竹竿與這一點O相距6m、與旗桿相距12m,則旗桿AB的高為7.5m.
如圖,小明用長為2.5m的竹竿CD做測量工具,測量學校旗桿AB的高度,移動竹竿,使竹竿、旗桿的頂端的影子恰好落在地面的同一點O.此時,竹竿與這一點O相距6m、與旗桿相距12m,則旗桿AB的高為7.5m.查看答案和解析>>
科目:初中數(shù)學 來源: 題型:選擇題
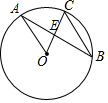 如圖,已知⊙O的半徑為2,點A、B、C為圓上三點,且OA∥BC,則$\frac{1}{CE}-\frac{1}{BC}$的值是( )
如圖,已知⊙O的半徑為2,點A、B、C為圓上三點,且OA∥BC,則$\frac{1}{CE}-\frac{1}{BC}$的值是( )| A. | 2 | B. | $\frac{1}{2}$ | C. | $\frac{3}{2}$ | D. | $\frac{2}{3}$ |
查看答案和解析>>
科目:初中數(shù)學 來源: 題型:解答題
查看答案和解析>>
科目:初中數(shù)學 來源: 題型:解答題
查看答案和解析>>
科目:初中數(shù)學 來源: 題型:選擇題
 如圖所示,在圓⊙O內(nèi)有折線OAB,其中OA=8,AB=12,∠A=∠B=60°,則BC的長為( )
如圖所示,在圓⊙O內(nèi)有折線OAB,其中OA=8,AB=12,∠A=∠B=60°,則BC的長為( )| A. | 20 | B. | 19 | C. | 18 | D. | 16 |
查看答案和解析>>
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com