
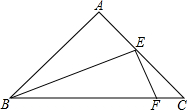
 如圖,在等腰三角形ABC中,AB=1,∠A=90°,點E為腰AC中點,點F在底邊BC上,且FE⊥BE,求△CEF的面積是$\frac{1}{24}$.
如圖,在等腰三角形ABC中,AB=1,∠A=90°,點E為腰AC中點,點F在底邊BC上,且FE⊥BE,求△CEF的面積是$\frac{1}{24}$. 分析 過C作CD⊥CE與EF的延長線交于D,構成直角三角形可證出Rt△ABE∽Rt△CED,然后證出其面積.
解答 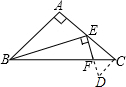 解:如圖,過C作CD⊥CE與EF的延長線交于D.
解:如圖,過C作CD⊥CE與EF的延長線交于D.
因為∠ABE+∠AEB=90°,∠CED+∠AEB=90°,所以∠ABE=∠CED.
于是Rt△ABE∽Rt△CED,
所以$\frac{{S}_{△CDE}}{{S}_{△EAB}}$=($\frac{CE}{AB}$)2=$\frac{1}{4}$.
又∠ECF=∠DCF=45°,所以CF是∠DCE的平分線,點F到CE和CD的距離相等,
所以$\frac{{S}_{△CEF}}{{S}_{△CDF}}$=$\frac{CE}{CD}$=2.
所以S△CEF=$\frac{2}{3}$S△CDE=$\frac{2}{3}$×$\frac{1}{4}$S△ABE=$\frac{2}{3}$×$\frac{1}{4}$×$\frac{1}{2}$S△ABC=$\frac{1}{24}$.
故答案是:$\frac{1}{24}$.
點評 本題考查了相似三角形的判定與性質,關鍵是作出輔助線,然后構成直角三角形,用相似三角形的性質求面積.


科目:初中數學 來源: 題型:解答題
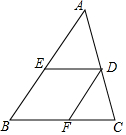 如圖,在△ABC中,AB=20,BC=12,D是AC上一點,過點D作DE∥BC交AB于E,作DF∥AB交BC于F,設四邊形BEDF為菱形.
如圖,在△ABC中,AB=20,BC=12,D是AC上一點,過點D作DE∥BC交AB于E,作DF∥AB交BC于F,設四邊形BEDF為菱形.查看答案和解析>>
科目:初中數學 來源: 題型:解答題
 已知:如圖,∠B=∠C=90°,M是BC的中點,且DM平分∠ADC.
已知:如圖,∠B=∠C=90°,M是BC的中點,且DM平分∠ADC.查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
科目:初中數學 來源: 題型:解答題

查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
| A. | 1或4 | B. | 1或$\frac{1}{4}$ | C. | -1或-4 | D. | -1或-$\frac{1}{4}$ |
查看答案和解析>>
科目:初中數學 來源: 題型:填空題
 如圖,正方體紙盒的棱長為4,點M、N分別在CD、HE上,CM=$\frac{1}{4}$CD,點N是HE的中點,將紙盒展開,若HC與NM的延長線交于點Q,則tan∠QNH=4.
如圖,正方體紙盒的棱長為4,點M、N分別在CD、HE上,CM=$\frac{1}{4}$CD,點N是HE的中點,將紙盒展開,若HC與NM的延長線交于點Q,則tan∠QNH=4.查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com