
 如圖在Rt△ABC中,∠C=90°,翻折∠C使點C落在斜邊AB上某一點D處,折痕為EF(點E,F分別在邊AC,BC上).
如圖在Rt△ABC中,∠C=90°,翻折∠C使點C落在斜邊AB上某一點D處,折痕為EF(點E,F分別在邊AC,BC上).分析 (1)①當AC=BC=2時,△ABC為等腰直角三角形;
②若△CEF與△ABC相似,分兩種情況:①若CE:CF=3:4,如圖1所示,此時EF∥AB,CD為AB邊上的高;②若CF:CE=3:4,如圖2所示.由相似三角形角之間的關系,可以推出∠A=∠ECD與∠B=∠FCD,從而得到CD=AD=BD,即D點為AB的中點;
(2)當點D是AB的中點時,△CEF與△ABC相似.可以推出∠CFE=∠A,∠C=∠C,從而可以證明兩個三角形相似.
解答 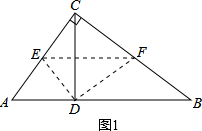 解:(1)若△CEF與△ABC相似.
解:(1)若△CEF與△ABC相似.
當AC=BC=2時,△ABC為等腰直角三角形,如圖1所示.
此時D為AB邊中點,AD=$\frac{\sqrt{2}}{2}$AC=$\sqrt{2}$;
故答案為:$\sqrt{2}$;
②若△CEF與△ABC相似,分兩種情況:
①若CE:CF=3:4,如圖1所示.
∵CE:CF=AC:BC,
∴EF∥AB.
由折疊性質可知,CD⊥EF,
∴CD⊥AB,即此時CD為AB邊上的高.
在Rt△ABC中,∵∠ACB=90°,AC=3,BC=4,
∴AB=$\sqrt{A{C}^{2}+B{C}^{2}}$=5,
∴cosA=$\frac{AC}{AB}$=$\frac{3}{5}$,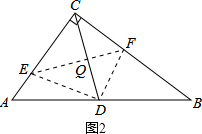 ∴AD=AC•cosA=3×$\frac{3}{5}$=1.8;
∴AD=AC•cosA=3×$\frac{3}{5}$=1.8;
②若CF:CE=3:4,如圖2所示.
∵△CEF∽△CBA,
∴∠CEF=∠B.
由折疊性質可知,∠CEF+∠ECD=90°,
又∵∠A+∠B=90°,
∴∠A=∠ECD,
∴AD=CD.
同理可得:∠B=∠FCD,CD=BD,
∴D點為AB的中點,
∴AD=$\frac{1}{2}$AB=$\frac{1}{2}$×5=2.5.
綜上所述,AD的長為1.8或2.5.
故答案為:1.8或2.5.
(2)當點D是AB的中點時,△CEF與△CBA相似.理由如下:
如答圖2所示,連接CD,與EF交于點Q.
∵CD是Rt△ABC的中線
∴CD=DB=$\frac{1}{2}$AB,
∴∠DCB=∠B.
由折疊性質可知,∠CQF=∠DQF=90°,
∴∠DCB+∠CFE=90°,
∵∠B+∠A=90°,
∴∠CFE=∠A,
又∵∠ACB=∠ACB,
∴△CEF∽△CBA.
點評 本題考查了相似三角形的判定與性質、直角三角形斜邊上的中線性質、等腰直角三角形的性質、勾股定理等知識;熟練掌握相似三角形的判定與性質是解決問題的關鍵.


科目:初中數學 來源: 題型:解答題
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
 如圖,方格紙中每個小正方形的邊長都是1,△ABC的三個頂點都在格點上,如果用(1,0)表示C點的位置,用(4,1)表示B點的位置,那么.
如圖,方格紙中每個小正方形的邊長都是1,△ABC的三個頂點都在格點上,如果用(1,0)表示C點的位置,用(4,1)表示B點的位置,那么.查看答案和解析>>
科目:初中數學 來源: 題型:解答題
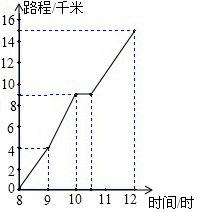 如圖為一位旅行者在早晨8時從城市出發到郊外所走的路程S(單位:千米)與時間t(單位:時)的變量關系的圖象.根據圖象回答問題:
如圖為一位旅行者在早晨8時從城市出發到郊外所走的路程S(單位:千米)與時間t(單位:時)的變量關系的圖象.根據圖象回答問題:查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com