

分析 (1)仔細分析題意根據折疊的性質及“好角”的定義即可作出判斷;
(2)因為經過三次折疊∠BAC是△ABC的好角,所以第三次折疊的∠A2B2C=∠C,由∠ABB1=∠AA1B1,∠AA1B1=∠A1B1C+∠C,又∠A1B1C=∠A1A2B2,∠A1A2B2=∠A2B2C+∠C,∠ABB1=∠A1B1C+∠C=∠A2B2C+∠C+∠C=3∠C,由此即可求得結果;
(3)根據好角的定義即可得出結果;
(4)根據好角的定義進行推理計算,即可得出結果.
解答 解:(1)△ABC中,∠B=2∠C,經過兩次折疊,∠BAC是△ABC的好角;
理由如下:小麗展示的情形二中,
∵沿∠BAC的平分線AB1折疊,
∴∠B=∠AA1B1;
又∵將余下部分沿∠B1A1C的平分線A1B2折疊,此時點B1與點C重合,
∴∠A1B1C=∠C;
∵∠AA1B1=∠C+∠A1B1C(外角定理),
∴∠B=2∠C;
故答案為:是;
(2)∠B=3∠C;
在△ABC中,沿∠BAC的平分線AB1折疊,剪掉重復部分;將余下部分沿∠B1A1C的平分線A1B2折疊,剪掉重復部分,將余下部分沿∠B2A2C的平分線A2B3折疊,點B2與點C重合,則∠BAC是△ABC的好角.
理由如下:∵根據折疊的性質知,∠B=∠AA1B1,∠C=∠A2B2C,∠A1B1C=∠A1A2B2,
∴根據三角形的外角定理知,∠A1A2B2=∠C+∠A2B2C=2∠C;
∵根據四邊形的外角定理知,∠BAC+∠B+∠AA1B1-∠A1B1C=∠BAC+2∠B-2C=180°,
根據三角形ABC的內角和定理知,∠BAC+∠B+∠C=180°,
∴∠B=3∠C;
由小麗展示的情形一知,當∠B=∠C時,∠BAC是△ABC的好角;
由小麗展示的情形二知,當∠B=2∠C時,∠BAC是△ABC的好角;
由小麗展示的情形三知,當∠B=3∠C時,∠BAC是△ABC的好角;
故若經過n次折疊∠BAC是△ABC的好角,則∠B與∠C(不妨設∠B>∠C)之間的等量關系為∠B=n∠C;
故答案為:∠B=3∠C;∠B=n∠C;
(3)∵60°=4×15°,15°+60°+105°=180°,
∴60°是三角形的好角;
同理:105°=7×15°,15°+60°+105°=180°,
∴105°是三角形的好角;
故答案為:60°,105°;
(4)10°,160°;由(2)知,∠B=n∠C,∠BAC是△ABC的好角,
因為最小角是10°是△ABC的好角,
根據好角定義,則可設另兩角分別為10m°,10mn°(其中m、n都是正整數).
由題意,得10m+10mn+10=180,所以m(n+1)=17.
因為m、n都是正整數,所以m與n+1是17的整數因子,
因此有:m=1,n+1=17;
所以m=1,n=16;
所以10m=10°,10mn=160°;
所以該三角形的另外兩個角的度數分別為:10°,160°;
故答案為:10°,160°.
點評 此題是三角形綜合題,主要考查了折疊問題,找規律,三角形的內角和定理,從折疊有限次數中找到規律是解本題的關鍵,也是難點.


科目:初中數學 來源: 題型:選擇題
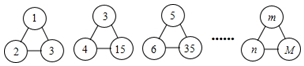
| A. | M=mn | B. | M=m(n+1) | C. | M=mn+1 | D. | M=n(m+1) |
查看答案和解析>>
科目:初中數學 來源: 題型:填空題
查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
| A. | ab=h2 | B. | a2+b2=2h2 | C. | $\frac{1}{a}$+$\frac{1}{b}$=$\frac{1}{h}$ | D. | $\frac{1}{{a}^{2}}$+$\frac{1}{{b}^{2}}$=$\frac{1}{{h}^{2}}$ |
查看答案和解析>>
科目:初中數學 來源: 題型:填空題

查看答案和解析>>
科目:初中數學 來源: 題型:解答題
 如圖所示,已知直線y=kx+m與x軸、y軸分別交于A、C兩點,拋物線y=-x2+bx+c經過A、C兩點,點B是拋物線與x軸的另一個交點,當x=-$\frac{1}{2}$時,y取最大值$\frac{25}{4}$.
如圖所示,已知直線y=kx+m與x軸、y軸分別交于A、C兩點,拋物線y=-x2+bx+c經過A、C兩點,點B是拋物線與x軸的另一個交點,當x=-$\frac{1}{2}$時,y取最大值$\frac{25}{4}$.查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com