Question

8．如圖所示，已知直線y=kx+m與x軸、y軸分別交于A、C兩點，拋物線y=-x²+bx+c經過A、C兩點，點B是拋物線與x軸的另一個交點，當x=-$\frac{1}{2}$時，y取最大值$\frac{25}{4}$．
（1）求拋物線和直線的解析式；
（2）設點P是直線AC上一點，且S_△ABP：S_△BPC=1：3，求點P的坐標；
（3）若直線y=$\frac{1}{2}$x+a與（1）中所求的拋物線交于M、N兩點，問：
①是否存在a的值，使得∠MON=90°？若存在，求出a的值；若不存在，請說明理由；
②猜想當∠MON＞90°時，a的取值范圍（不寫過程，直接寫結論）．

Answer 1

分析 （1）先根據直線的解析式求出A、C的坐標，然后將A、C的坐標代入拋物線中即可求出拋物線的解析式，進而可根據拋物線的解析式求出B點的坐標．
（2）根據等高三角形的面積比等于底邊比，因此兩三角形的面積比實際是AP：PC=1：3，即3AP=PC，可先求出AC的長，然后分情況討論：
①當P在線段AC上時，AP+PC=AC，3AP=PC，據此可求出AP的長，然后根據∠CAB的三角函數值或通過構建相似三角形可求出P點的坐標．
②當P在CA的延長線上時，CP-AP=AC，3AP=PC，據此可求出AP的長，后面同①．
（3）①設直線y=$\frac{1}{2}$x+a與拋物線y=-x²-x+6的交點為M（x_M，y_M），N（x_N，y_N）（M在N左側），由Rt△MM′O∽Rt△ON′N，推出 $\frac{MM′}{ON′}$=$\frac{OM′}{NN′}$，即MM′•NN′=ON′•OM′，推出-x_M•x_N=y_M•y_N，由方程組消去y整理，得：x²+$\frac{3}{2}$x+a-6=0，再利用根與系數關系，列出方程即可解決問題．
②利用①的結果即可判斷．

解答 解：（1）當x=0時，y=6，
∴C（0，6），
當y=0時，x=-3，
∴A（-3，0），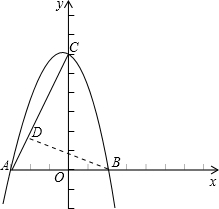
∵拋物線y=-x²+bx+c經過點A、C，
∴$\left\{\begin{array}{l}{-9-3b+\\;c=0}\\{c=6}\end{array}\right.$，
解得：$\left\{\begin{array}{l}{b=-1}\\{c=6}\end{array}\right.$．
∴拋物線的解析式為y=-x²-x+6，
當y=0時，整理得x²+x-6=0，
解得：x₁=2，x₂=-3，
∴點B（2，0）．

（2）過點B作BD⊥AC，D為垂足，
∵S_△ABP：S_△BPC=1：3，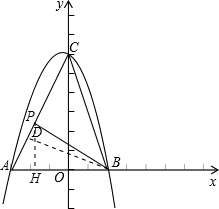
∴$\frac{\frac{1}{2}•AP•BD}{\frac{1}{2}•PC•BD}$=$\frac{1}{3}$，
∴AP：PC=1：3
由勾股定理，得AC=$\sqrt{O{A}^{2}+O{C}^{2}}$=3 $\sqrt{5}$，
當點P為線段AC上一點時，過點P作PH⊥x軸，點H為垂足，
∵PH∥OC，
∴$\frac{PH}{OC}$=$\frac{AP}{PC}$=$\frac{1}{4}$，
∴PH=$\frac{3}{2}$，
∴$\frac{3}{2}$=2x+6，
∴x=-$\frac{9}{4}$，
∴點P（-$\frac{9}{4}$，$\frac{3}{2}$）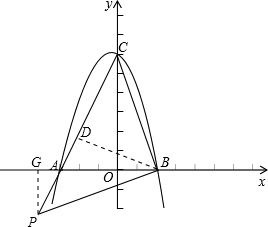
當點P在CA延長線時，作PG⊥x軸，點G為垂足
∵AP：PC=1：3
∴AP：AC=1：2，
∴$\frac{PG}{OC}$=$\frac{AP}{AC}$=$\frac{1}{2}$，
∴PG=3，
∴-3=2x+6
x=-$\frac{9}{2}$，
∴點P（-$\frac{9}{2}$，-3）．

（3）①存在a的值，使得∠MON=90°，
設直線y=$\frac{1}{2}$x+a與拋物線y=-x²-x+6的交點為M（x_M，y_M），N（x_N，y_N）（M在N左側）
則 $\left\{\begin{array}{l}{{x}_{1}={x}_{M}}\\{{y}_{1}={y}_{M}}\end{array}\right.$為方程組 $\left\{\begin{array}{l}{y=\frac{1}{2}x+a}\\{y=-{x}^{2}-x+6}\end{array}\right.$的解
分別過點M、N作MM’⊥x軸，NN′⊥x軸，點M、N為垂足．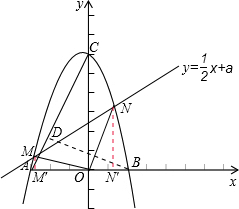
∴M′（x_M，0），N′（x_N，0），
∴OM′=-x_MON′=x_N
∵∠MON=90°，
∴∠MOM′+∠NON′=90°，
∵∠M′MO+∠MOM′=90°，
∴∠M’MO=∠NON’
∴Rt△MM′O∽Rt△ON′N，
∴$\frac{MM′}{ON′}$=$\frac{OM′}{NN′}$，
∴MM′•NN′=ON′•OM′，
∴-x_M•x_N=y_M•y_N，
由方程組消去y整理，得：x²+$\frac{3}{2}$x+a-6=0．
∴x_M、x_N是方程x²+$\frac{3}{2}$x+a-6=0的兩個根，
由根與系數關系得，x_M+x_N=-$\frac{3}{2}$，x_M•x_N=a-6
又∵y_M•y_N=（ $\frac{1}{2}$x_M+a）（ $\frac{1}{2}$x_N+a）=$\frac{1}{4}$x_M•x_N+$\frac{a}{2}$（x_M+x_N）+a²=$\frac{1}{4}$（a-6）-$\frac{3}{4}$a+a²
∴-（a-6）=$\frac{1}{4}$（a-6）-$\frac{3}{4}$a+a²，
整理，得2a²+a-15=0
解得a₁=-3，a₂=$\frac{5}{2}$，
∴存在a值，使得∠MON=90°，其值為a=-3或a=$\frac{5}{2}$．
②由①可知，當∠MON＞90°時，a的取值范圍為-3＜a＜$\frac{5}{2}$．

點評 本題考查待定系數法求二次函數解析式、圖形面積的計算方法、三角形相似、函數圖象交點、一元二次方程根與系數關系等重要知識點，綜合性強，能力要求較高．考查學生分類討論，數形結合的數學思想方法．