
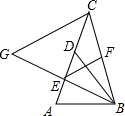
 在△ABC中,點(diǎn)D在邊AC上,BD=BA,點(diǎn)E是AD的中點(diǎn),點(diǎn)F是BC的中點(diǎn).
在△ABC中,點(diǎn)D在邊AC上,BD=BA,點(diǎn)E是AD的中點(diǎn),點(diǎn)F是BC的中點(diǎn).分析 (1)由BD=BA,E是AD的中點(diǎn),根據(jù)等腰三角形三線合一的性質(zhì)得出BE⊥AD,再根據(jù)直角三角形斜邊上中線等于斜邊的一半即可證明EF=$\frac{1}{2}$BC;
(2)先由CG∥EF,根據(jù)平行線的性質(zhì)得出∠G=∠FEB,又EF=$\frac{1}{2}$BC=BF,根據(jù)等邊對(duì)等角得出∠FEB=∠CBE,等量代換得到∠G=∠CBE,那么GC=BC,即△BCG是等腰三角形.
解答 證明:(1)∵BD=BA,E是AD的中點(diǎn),
∴BE⊥AD,
∴△EBC為直角三角形.
∵F是BC的中點(diǎn),
∴EF是直角三角形斜邊上中線 ∴EF=$\frac{1}{2}$BC;
∴EF=$\frac{1}{2}$BC;
(2)∵CG∥EF,
∴∠G=∠FEB,
∵EF=$\frac{1}{2}$BC=BF,
∴∠FEB=∠CBE,
∴∠G=∠CBE,
∴GC=BC,
∴△BCG是等腰三角形.
點(diǎn)評(píng) 本題考查了直角三角形斜邊上中線等于斜邊的一半的性質(zhì),等腰三角形的判定與性質(zhì).得出BE⊥AD是證明(1)的關(guān)鍵;得出∠G=∠CBE是證明(2)的關(guān)鍵.


 期末金牌卷系列答案
期末金牌卷系列答案 輕松課堂標(biāo)準(zhǔn)練系列答案
輕松課堂標(biāo)準(zhǔn)練系列答案
| 年級(jí) | 高中課程 | 年級(jí) | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:初中數(shù)學(xué) 來源: 題型:解答題
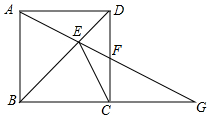 如圖,ABCD是正方形,G是BC延長(zhǎng)線上一點(diǎn),AG交BD于E,交CD于F,求證:CE與△CFG的外接圓相切.
如圖,ABCD是正方形,G是BC延長(zhǎng)線上一點(diǎn),AG交BD于E,交CD于F,求證:CE與△CFG的外接圓相切.查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:選擇題
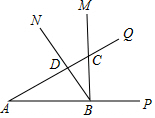 如圖,∠PAQ=∠MBN=30°,∠MBN的頂點(diǎn)B在射線AP上,射線BM和射線BN分別交射線AQ于點(diǎn)C、D,當(dāng)∠MBN繞點(diǎn)B轉(zhuǎn)動(dòng)時(shí).若AB=2$\sqrt{3}$,則CA•CD的最小值是( )
如圖,∠PAQ=∠MBN=30°,∠MBN的頂點(diǎn)B在射線AP上,射線BM和射線BN分別交射線AQ于點(diǎn)C、D,當(dāng)∠MBN繞點(diǎn)B轉(zhuǎn)動(dòng)時(shí).若AB=2$\sqrt{3}$,則CA•CD的最小值是( )| A. | 3 | B. | $\sqrt{3}$ | C. | 4 | D. | 12 |
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:解答題
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:解答題

查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:選擇題
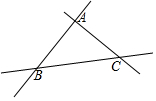 如圖是三條兩兩相交的筆直公路,現(xiàn)欲修建一個(gè)加油站,使它到三條公路的距離相等,這個(gè)加油站應(yīng)建在( )
如圖是三條兩兩相交的筆直公路,現(xiàn)欲修建一個(gè)加油站,使它到三條公路的距離相等,這個(gè)加油站應(yīng)建在( )| A. | △ABC三邊的中線的交點(diǎn)上 | B. | △ABC三邊垂直平分線的交點(diǎn)上 | ||
| C. | △ABC三條邊高的交點(diǎn)上 | D. | △ABC三內(nèi)角平分線的交點(diǎn)上 |
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:填空題
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:解答題
 如圖,△ABC的頂點(diǎn)坐標(biāo)分別為A(4,5),B(2,3),C(5,1).
如圖,△ABC的頂點(diǎn)坐標(biāo)分別為A(4,5),B(2,3),C(5,1).查看答案和解析>>
百度致信 - 練習(xí)冊(cè)列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺(tái) | 網(wǎng)上有害信息舉報(bào)專區(qū) | 電信詐騙舉報(bào)專區(qū) | 涉歷史虛無主義有害信息舉報(bào)專區(qū) | 涉企侵權(quán)舉報(bào)專區(qū)
違法和不良信息舉報(bào)電話:027-86699610 舉報(bào)郵箱:58377363@163.com