
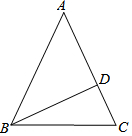
 如圖,在等腰△ABC中,AB=AC,BD為高.(從下列問題中任選一問作答)
如圖,在等腰△ABC中,AB=AC,BD為高.(從下列問題中任選一問作答)分析 (1)設∠ABD=x°,則∠A=(90-x)°,∠C=(120-x)°,根據三角形的內角和即可得到結論;
(2)根據直角三角形的性質得到BD=4,BC=5,求得CD=3,設AD為x,則AB=AC=3+x,根據勾股定理即可得到結論.
解答 解:(1)∵AB=AC,∴∠ABC=∠C,
設∠ABD=x°,
則∠A=(90-x)°,∠C=(120-x)°,
在△ABC中:∠A+∠C+∠ABC=180°,
即90-x+2(120-x)=180,
解得x=50°,
則∠A=90-x=40°;
(2)∵BD為高.∴△ADC為直角三角形,
∵BD=4,BC=5,
∴CD=3,
設AD為x,則AB=AC=3+x,
在直角三角形△ADB中,AD2+BD2=AB2,
即,x2+42=(x+3)2,
解得x=$\frac{7}{6}$,
S△ABC=AC×BD×$\frac{1}{2}$=$\frac{25}{3}$.
點評 本題考查了等腰三角形的性質,三角形的面積的計算,熟記等腰三角形的性質是解題的關鍵.


科目:初中數學 來源: 題型:解答題
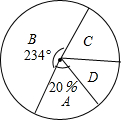 某中學為了科學建設“學生健康成長工程”,隨機抽取了部分學生家庭對其家長進行了主題“周末孩子在家您關心了嗎?”的調查問卷,將收回的調查問卷進行了分析整理,得到了如下的樣本統計圖表和扇形統計圖:
某中學為了科學建設“學生健康成長工程”,隨機抽取了部分學生家庭對其家長進行了主題“周末孩子在家您關心了嗎?”的調查問卷,將收回的調查問卷進行了分析整理,得到了如下的樣本統計圖表和扇形統計圖:| 代號 | 情況分類 | 家庭數 |
| A | 帶孩子玩且關心其作業完成情況 | 8 |
| B | 只關心其作業完成情況 | m |
| C | 只帶孩子玩 | 4 |
| D | 既不帶孩子玩也不關心其作業完成情況 | n |
查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
| A. | 1米 | B. | 2米 | C. | 4米 | D. | 5米 |
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
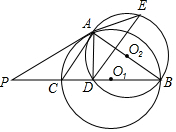 如圖,⊙O1與⊙O2相交于A、B兩點,AB是⊙O2的直徑,過點A作⊙O1的切線交⊙O2于點E,并與BO1的延長線交于點P,BP分別與⊙O1、⊙O2交于點C、D.求證:
如圖,⊙O1與⊙O2相交于A、B兩點,AB是⊙O2的直徑,過點A作⊙O1的切線交⊙O2于點E,并與BO1的延長線交于點P,BP分別與⊙O1、⊙O2交于點C、D.求證:查看答案和解析>>
科目:初中數學 來源: 題型:解答題

查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com