

分析 (1)根據兩角對應相等兩三角形相似即可證明.
(2)結論:$\frac{EF}{AM}$=$\frac{BC}{AB}$.如圖2中,過點B作BG∥EF交CD于G,首先證明四邊形BEFG是平行四邊形,推出BG=EF,由△GBC∽△MAB,得$\frac{BG}{AM}$=$\frac{BC}{AB}$,由此即可證明.
(3)如圖3中,過點D作平行于AB的直線交過點A平行于BC的直線于R,交BC的延長線于S,連接AC,則四邊形ABSR是平行四邊形.由(2)中結論可得:$\frac{DN}{AM}$=$\frac{BS}{AB}$,想辦法求出BS即可解決問題.
解答 解:(1)如圖1中,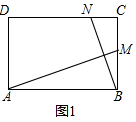
∵四邊形ABCD是矩形,
∴∠ABC=∠C=90°
∴∠NBA+∠NBC=90°,
∵AM⊥BN,
∴∠MAB+∠NBA=90°,
∴∠NBC=∠MAB,
∴△BCN∽△ABM,
∴$\frac{BN}{AM}$=$\frac{BC}{AB}$.
(2)結論:$\frac{EF}{AM}$=$\frac{BC}{AB}$.
理由:如圖2中,過點B作BG∥EF交CD于G,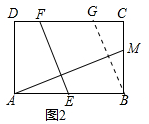
∵四邊形ABCD是矩形,
∴AB∥CD,
∴四邊形BEFG是平行四邊形,
∴BG=EF,
∵EF⊥AM,
∴BG⊥AM,
∴∠GBA+∠MAB=90°,
∵∠ABC=∠C=90°,
∴∠GBC+∠GBA=90°,
∴∠MAB=∠GBC,
∴△GBC∽△MAB,
∴$\frac{BG}{AM}$=$\frac{BC}{AB}$,
∴$\frac{EF}{AM}$=$\frac{BC}{AB}$.
(3)如圖3中,過點D作平行于AB的直線交過點A平行于BC的直線于R,交BC的延長線于S,連接AC,則四邊形ABSR是平行四邊形.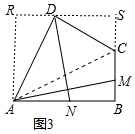
∵∠ABC=90°,
∴四邊形ABSR是矩形,
∴∠R=∠S=90°,RS=AB=10,AR=BS,
∵AM⊥DN,
∴由(2)中結論可得:$\frac{DN}{AM}$=$\frac{BS}{AB}$,
∵AB=AD,CB=CD,AC=AC,
∴△ACD≌△ACB,
∠ADC=∠ABC=90°,
∴∠SDC+∠RDA=90°,
∵∠RAD+∠RDA=90°,
∴∠RAD=∠SDC,
∴△RAD∽△SDC,
∴∴$\frac{CD}{AD}$=$\frac{SC}{RD}$,設SC=x,
∴$\frac{5}{10}$=$\frac{x}{RD}$,
∴RD=2x,DS=10-2x,
在Rt△CSD中,∵CD2=DS2+SC2,
∴52=(10-2x)2+x2,
∴x=3或5(舍棄),
∴BS=5+x=8,
∴$\frac{DN}{AM}$=$\frac{BS}{AB}$=$\frac{8}{10}$=$\frac{4}{5}$.
點評 本題考查相似三角形綜合題、矩形的判定和性質、平行四邊形的判定和性質、勾股定理等知識,解題的關鍵是正確尋找相似三角形,學會添加常用輔助線,構造相似三角形解決問題,屬于中考壓軸題.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小學生10分鐘應用題系列答案
小學生10分鐘應用題系列答案科目:初中數學 來源: 題型:解答題
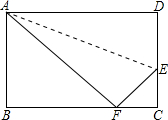 如圖所示,沿AE折疊長方形ABCD使點D恰好落在BC邊上的點F處.已知AB=8cm,BC=10cm.
如圖所示,沿AE折疊長方形ABCD使點D恰好落在BC邊上的點F處.已知AB=8cm,BC=10cm.查看答案和解析>>
科目:初中數學 來源: 題型:解答題
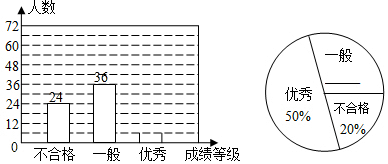
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
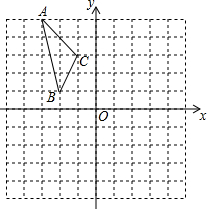 如圖,在平面直角坐標系中,已知△ABC的三個頂點的坐標分別為A(-3,5),B(-2,1),C(-1,3).
如圖,在平面直角坐標系中,已知△ABC的三個頂點的坐標分別為A(-3,5),B(-2,1),C(-1,3).查看答案和解析>>
科目:初中數學 來源: 題型:解答題
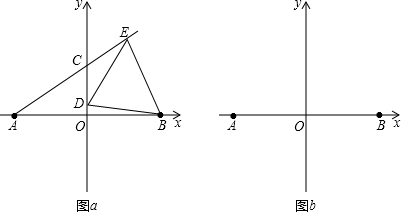
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
| 進價(元/只) | 售價(元/只) | |
| 甲型 | 25 | 30 |
| 乙型 | 45 | 60 |
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
 如圖,在△ABC中,D是AB中點,聯結CD.
如圖,在△ABC中,D是AB中點,聯結CD.查看答案和解析>>
科目:初中數學 來源: 題型:填空題
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com