Question

16．在平面直角坐標系xOy中，點A（a，0），點B（b，0）是x軸上兩點，其中a²+2ab+b²+|b-4|=0，點C，D都在y軸上，E在射線AC上（不與點A重合），DB=DE，連結BE．
（1）求A、B的坐標；
（2）如圖a，若C在y軸正半軸，D在線段OC上，當∠CAO=30°時，求證：△BDE為等邊三角形；（提示：連結AD…）
（3）當BD⊥DE時，在圖b中畫出示意圖，設E（m，n），若mn=2，求$\frac{n}{m}$+$\frac{m}{n}$的值．

Answer 1

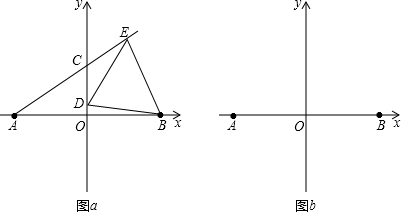
分析 （1）由a²+2ab+b²+|b-4|=0，得出（a+b）²+|b-4|=0，再根據非負數的性質，得出a=-4，b=4，即可得到A（-4，0），B（4，0）；
（2）連接AD并延長至F，根據等腰三角形的性質以及三角形外角性質，即可得出∠BDF=∠DAO+∠DBO=2∠DAO，∠EDF=2∠DAE，進而得到∠EDB=60°，再根據DE=DB，即可得出△BDE為等邊三角形；
（3）分兩種情況進行討論：①當C在y軸正半軸時，②當C在y軸負半軸時，分別判定全等三角形，根據全等三角形的對應邊相等，分別求得n-m=4，m+n=-4，再根據mn=2，求得$\frac{n}{m}$+$\frac{m}{n}$的值即可．

解答 解：（1）∵a²+2ab+b²+|b-4|=0，
∴（a+b）²+|b-4|=0，
  又∵（a+b）²≥0，|b-4|≥0，
∴（a+b）²=0，|b-4|=0，
∴a=-4，b=4，
∴A（-4，0），B（4，0）；

（2）證明：如圖a，連接AD并延長至F，
∵A（-4，0），B（4，0），
∴OA=OB，
∵OD⊥AB，
∴DA=DB，
∴∠DAO=∠DBO，
∴∠BDF=∠DAO+∠DBO=2∠DAO，
∵DA=DB，DE=DB，
∴DA=DE，
同理可得∠EDF=2∠DAE，
∴∠BDF+∠EDF=2∠DAE+2∠DAO=2∠CAO=60°，
即∠EDB=60°，
又∵DE=DB，
∴△BDE為等邊三角形；

（3）分兩種情況：
①當C在y軸正半軸時，如圖b所示，過點E作EG⊥y軸于點G，則∠GED+∠GDE=90°，
∵DE⊥DB，
∴∠ODB+∠GDE=90°，
∴∠GED=∠ODB，
又∵∠DGE=∠DOB=90°，DE=DB，
∴在△DGE和△BOD中，
$\left\{\begin{array}{l}{∠GED=∠ODB}\\{∠DGE=∠DOB}\\{DE=DB}\end{array}\right.$，
∴△DGE≌△BOD（AAS）
∴OD=EG，DG=OB=4，
∵E（m，n），
∴OD=EG=m，OG=n，
由OG-OD=DG，得n-m=4，
∵mn=2，
∴$\frac{n}{m}$+$\frac{m}{n}$=$\frac{{m}^{2}+{n}^{2}}{mn}$=$\frac{（n-m）^{2}+2mn}{mn}$=$\frac{{4}^{2}+2×2}{2}$=10；

②當C在y軸負半軸時，如圖c所示，過點E作EG⊥y軸于點G，
同理可得，△DGE≌△BOD，
∴OD=EG，DG=OB=4，
∵E（m，n），
∴OD=EG=-m，OG=-n，
由OD+OG=DG，得-m+（-n）=4，則m+n=-4，
∵mn=2，
∴$\frac{n}{m}$+$\frac{m}{n}$=$\frac{{m}^{2}+{n}^{2}}{mn}$=$\frac{（m+n）^{2}-2mn}{mn}$=$\frac{（-4）^{2}-2×2}{2}$=6，
綜上所述，$\frac{n}{m}$+$\frac{m}{n}$的值為10或6．

點評 本題屬于三角形綜合題，主要考查了非負數的性質，全等三角形的判定與性質，三角形外角性質以及等邊三角形的判定的綜合應用，解決問題的關鍵是作輔助線構造全等三角形，運用全等三角形的對應邊相等進行計算求解．解題時注意：有一個角是60°的等腰三角形是等邊三角形．