

分析 (1)①利用等腰三角形的三線合一得出點B的橫坐標為3,再利用勾股定理即可得出點B的縱坐標為4即可;
②先判斷出△BOC是等腰三角形,即可得出點C在線段OB的垂直平分線上,先確定出直線OB解析式和OB中點坐標,即可得出CD的解析式即可;
(2)直接判斷出△OBC≌△ABD即可得出結論;
(3)證出∠BEO=∠BAM,EB=OB=5,得出AM=ME,OE=$\sqrt{E{A}^{2}-O{A}^{2}}$=8,因此AM=EM=8-m,由勾股定理得出方程,解方程求出m的值,即可得出結論.
解答 (1):①過B作BH⊥OA于點H,如圖1所示:
∵OB=BA=5,OA=6,
∴OH=$\frac{1}{2}$OA=3,
∴BH=4,
∴B(3,4);
②若BD∥OC,則點D在BH上,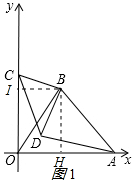
∵∠COB=∠OBH=$\frac{1}{2}$∠OBA,∠CBD=∠OBA,
∴∠COB=∠OBC,
∴OC=BC,
過BI⊥OC于點I,
OI=BH=4,IC=4-k
∴(4-k)2+32=k2,
解得:k=$\frac{25}{8}$;
(2)證明:∵∠CBD=∠OBA,
∴∠CBO=∠DBA,
∴BC=BD,OB=AB,
在△OBC和△ABD中,$\left\{\begin{array}{l}{BC=BD}&{\;}\\{∠CBO=∠DBA}&{\;}\\{OB=BA}&{\;}\end{array}\right.$,
∴△OBC≌△ABD(SAS),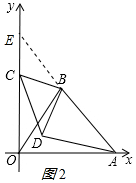
∴OC=AD.
(3)解:點M的位置不變;理由如下:
延長AB交y軸于點E,如圖2所示:
由(2)知△OBC≌△ABD,
得:∠BOE=∠BAM,
∵OB=BA,∴∠BOA=∠BAO,
∵∠BOE+∠BOA=90°,∠BAO+∠BEO=90°,
∴∠BOE=∠BEO,
∴∠BEO=∠BAM,EB=OB=5
∴AM=ME,OE=$\sqrt{E{A}^{2}-O{A}^{2}}$=8,
∴AM=EM=8-m,
∵OM2+OA2=AM2,
∴(8-m)2=m2+62,
解得:m=$\frac{7}{4}$,
∴點M的位置不變,m=$\frac{7}{4}$.
點評 此題是三角形綜合題,主要考查了等腰三角形的性質和判定,全等三角形的性質和判定,勾股定理,平行線的性質等知識;解本題的關鍵是判斷出OC=AD,是一道中等難度的題目.


科目:初中數學 來源: 題型:解答題
| 星期 | 一 | 二 | 三 | 四 | 五 | 六 | 日 |
| 增減 | +5 | -2 | -4 | +12 | -10 | +16 | -9 |
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
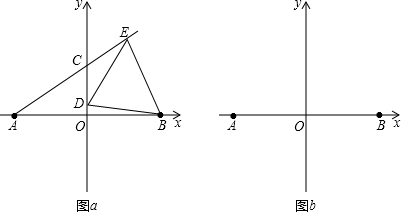
 如圖,已知數軸上有A、B、C三個點,它們表示的數分別是a、b和8,O是原點,且(a+20)2+|b+10|=0.
如圖,已知數軸上有A、B、C三個點,它們表示的數分別是a、b和8,O是原點,且(a+20)2+|b+10|=0.查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
科目:初中數學 來源: 題型:填空題
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com