
 如圖,在△ABC中,D是AB中點,聯結CD.
如圖,在△ABC中,D是AB中點,聯結CD.分析 (1)求出AD=$\frac{1}{2}$AB=5,證明△ACD∽△ABC,得出$\frac{AC}{AB}=\frac{AD}{AC}$,即可得出結果;
(2)由平行線的性質得出AE=EC,由向量的定義容易得出結果.
解答 解:(1)∵D是AB中點,
∴AD=$\frac{1}{2}$AB=5,
∵∠ACD=∠B,∠A=∠A,
∴△ACD∽△ABC,
∴$\frac{AC}{AB}=\frac{AD}{AC}$,
∴AC2=AB•AD=10×5=50,
∴AC=$\sqrt{50}$=5$\sqrt{2}$;
(2)如圖所示:∵DE∥BC,D是AB的中點,
∴AD=DB,AE=EC,
∵$\overrightarrow{DE}$=$\overrightarrow{a}$,$\overrightarrow{DC}$=$\overrightarrow{b}$,
∴$\overrightarrow{AE}=\overrightarrow{EC}$=$\overrightarrow{DC}-\overrightarrow{DE}$=$\overrightarrow{b}-\overrightarrow{a}$,
∴$\overrightarrow{AC}=-2\overrightarrow{a}+2\overrightarrow{b}$,
∵$\overrightarrow{AD}=\overrightarrow{AE}-\overrightarrow{DE}$=$\overrightarrow{b}-\overrightarrow{a}-\overrightarrow{a}$=$\overrightarrow{b}-2\overrightarrow{a}$,
∴$\overrightarrow{AB}=-4\overrightarrow{a}+2\overrightarrow{b}$.
點評 本題考查了相似三角形的判定與性質、平面向量、平行線的性質;熟練掌握相似三角形的判定與性質是解決問題的關鍵.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小學生10分鐘應用題系列答案
小學生10分鐘應用題系列答案科目:初中數學 來源: 題型:解答題

查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
 某校為了更好的開展“學校特色體育教育”,從全校八年級各班隨機抽取了60學生,進行各項體育項目的測試,了解他們的身體素質情況.下表是整理樣本數據,得到的關于每個個體的測試成績的部分統計表、圖:
某校為了更好的開展“學校特色體育教育”,從全校八年級各班隨機抽取了60學生,進行各項體育項目的測試,了解他們的身體素質情況.下表是整理樣本數據,得到的關于每個個體的測試成績的部分統計表、圖:| 成績 | 劃記 | 頻數 | 頻率 |
| 優秀 | 正正正 | a | 0.3 |
| 良好 | 正正正正正正 | 30 | b |
| 合格 | 正 | 9 | 0.15 |
| 不合格 |   | c | d |
| 合計 |
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
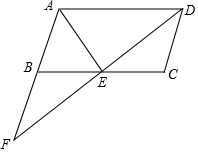 如圖,在?ABCD中,E是BC邊的中點,DE與AB的延長線交于點F.
如圖,在?ABCD中,E是BC邊的中點,DE與AB的延長線交于點F.查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com