
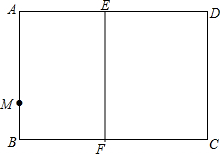
 如圖,在矩形紙片ABCD中,AB=4,BC=5,點E在AD邊上,EF⊥BC,垂足為F,點M在AB邊上,BM=1,沿過點M的直線折疊該紙片,使點A落在線段EF上的點A'處,折痕為 MN,點N在AD邊上.
如圖,在矩形紙片ABCD中,AB=4,BC=5,點E在AD邊上,EF⊥BC,垂足為F,點M在AB邊上,BM=1,沿過點M的直線折疊該紙片,使點A落在線段EF上的點A'處,折痕為 MN,點N在AD邊上.分析 (1)以M為圓心,MA長為半徑畫弧,交EF于A',作∠AMA'的角平分線,交AD于N,連接NA',MA',則MN是折痕;
(2)過點M作MH⊥EF于H,得出BF=MH=AE=1.8,BM=GF=1,EG=AM=3,根據勾股定理求得A'G,再設AN=x,則NE=1.8-x,NA'=x,在Rt△A'EN中,根據勾股定理得到(1.8-x)2+0.62=x2,求得AN的長,最后根據勾股定理求得MN的長即可;
(3)分情況討論即可,當BF<2$\sqrt{2}$時,有一條折痕;當2$\sqrt{2}$≤BF<3時,有兩條折痕;當BF=3時,有一條折痕;當BF>3時,無折痕.
解答 解:(1)如圖所示,折痕MN即為所求;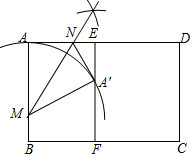 ;
;
(2)過點M作MG⊥EF于G,則BF=MG=AE=1.8,BM=GF=1,EG=AM=3,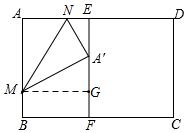
由折疊得,MA'=MA=3,
∴Rt△MA'G中,A'G=$\sqrt{{3}^{2}-1.{8}^{2}}$=2.4,
∴EA'=3-2.4=0.6,
設AN=x,則NE=1.8-x,NA'=x,
∴Rt△A'EN中,(1.8-x)2+0.62=x2,
解得x=1,
∴AN=1,
∴Rt△AMN中,MN=$\sqrt{A{M}^{2}+A{N}^{2}}$=$\sqrt{10}$;
(3)連接MF,因為當MF=MA'=3時,Rt△BMF中,BF=$\sqrt{{3}^{2}-{1}^{2}}$=2$\sqrt{2}$,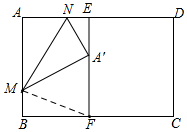
故當BF<2$\sqrt{2}$時,有一條折痕;
因為當MA'⊥EF時,BF=MA'=3,
故當2$\sqrt{2}$≤BF<3時,有兩條折痕;
當BF=3時,有一條折痕;
當BF>3時,無折痕.
點評 本題主要考查了矩形的性質以及折疊的性質,解題時注意:折疊是一種對稱變換,它屬于軸對稱,折疊前后圖形的形狀和大小不變,位置變化,對應邊和對應角相等.


科目:初中數學 來源: 題型:解答題
 如圖所示,在Rt△ABC中,∠C=90°,∠B=60°.
如圖所示,在Rt△ABC中,∠C=90°,∠B=60°.查看答案和解析>>
科目:初中數學 來源: 題型:解答題
 某校組織全校2 000名學生進行了環保知識競賽.為了解成績的分布情況,隨機抽取了部分學生的成績(得分取整數,滿分為100分),并繪制了頻數分布表和頻數分布直方圖(不完整):
某校組織全校2 000名學生進行了環保知識競賽.為了解成績的分布情況,隨機抽取了部分學生的成績(得分取整數,滿分為100分),并繪制了頻數分布表和頻數分布直方圖(不完整):| 分組 | 頻數 | 頻率 |
| 50.5~60.5 | 20 | 0.05 |
| 60.5~70.5 | 48 | △ |
| 70.5~80.5 | △ | 0.20 |
| 80.5~90.5 | 104 | 0.26 |
| 90.5~100.5 | 148 | △ |
| 合計 | △ | 1 |
查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
 如圖,△ABC中,∠B=90°,AB=1,BC=2,則sinA=( )
如圖,△ABC中,∠B=90°,AB=1,BC=2,則sinA=( )| A. | $\frac{{\sqrt{5}}}{2}$ | B. | $\frac{1}{2}$ | C. | $\frac{{2\sqrt{5}}}{5}$ | D. | $\frac{{\sqrt{5}}}{5}$ |
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com