Question

2．在△ABC與△ADE中，∠BAC=∠DAE=90°，AB=AC，AD=AE，延長DE交BC于點F，連接DC，BE．
（1）如圖1，當點B，A，D在同一直線上時，且∠ABE=30°，AE=2，求BF的長．
（2）如圖2，當∠BEA=90°時，求證：BF=CF．
（3）如圖3，當點E在∠ABC的平分線上時，BE交DC于點G，請直接寫出EG、DG、CG之間的數量關系．

Answer 1

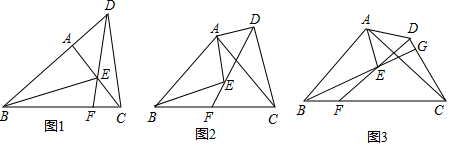
分析 （1）先根據直角三角形30°角的性質得：BE=2AE=4，由△ADE是等腰直角三角形，計算DE的長，同時得
△BDF也是等腰三角形，設BF=x，Rt△BEF中，由勾股定理列方程解出x的值即可；
（2）如圖2，連接AF，先證明△ADC≌△AEB，得∠ADC=∠AEB=90°，證明∠ADE=∠ACB=45°，可知A、F、C、D四點共圓，根據四點共圓的性質：圓內接四邊形的對角互補得：∠ADC+∠AFC=180°，則∠AFC=90°，由等腰三角形三線合一得：BF=CF；
（3）結論：DG+EG=$\sqrt{2}$CG，作輔助線，構建直角三角形和正方形，首先證明四邊形ANGM是正方形，由A、G、C、B四點共圓，推出∠AGO=∠ACB=45°，再利用四點共圓的性質推出CG=AG，由△AMD≌△ANE，推出NG=MG，可得EG+DG=$\sqrt{2}$CG．

解答 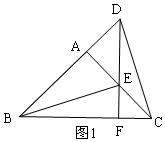（1）解：∵∠BAC=90°，∠ABE=30°，AE=2，
∴BE=2AE=4，
∵△ADE是等腰直角三角形，
∴DE=$\sqrt{2}$AE=2$\sqrt{2}$，
∵△ABC也是等腰三角形，
∴∠ABC=∠ADE=45°，
∴∠DFB=90°，BF=DF，
設BF=x，則EF=DF-DE=x-2$\sqrt{2}$，
在Rt△BEF中，由勾股定理得：${4}^{2}={x}^{2}+（x-2\sqrt{2}）^{2}$，
解得：x₁=$\sqrt{2}+\sqrt{6}$，x₂=$\sqrt{2}-\sqrt{6}$（舍），
∴BF=$\sqrt{2}+\sqrt{6}$；
（2）證明：如圖2，連接AF，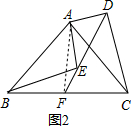
∵∠BAC=∠EAD=90°，
∴∠BAE+∠EAC=∠CAD+∠EAC，
∴∠BAE=∠CAD，
在△ABE和△ACD中，
∵$\left\{\begin{array}{l}{AB=AC}\\{∠BAE=∠CAD}\\{AE=AD}\end{array}\right.$，
∴△ADC≌△AEB（SAS），
∴∠ADC=∠AEB=90°，
∵△AED和△ABC是等腰直角三角形，
∴∠ADE=∠ACB=45°，
∴A、F、C、D四點共圓，
∴∠ADC+∠AFC=180°，
∴∠AFC=90°，
∴AF⊥BC，
∵AB=AC，
∴BF=CF；
（3）解：如圖3，DG+EG=$\sqrt{2}$CG，理由是：
過A作AN⊥BG于G，作AM⊥CD于M，連接AG，
同理得：△ABE≌△ACD，
∴∠ABO=∠ACD，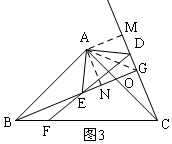
∴A、B、C、G四點共圓，
∴∠AGB=∠ACB=45°，∠OGC=∠BAO=90°，
∴∠BGD=90°，
∴∠NGA=∠AGD=45°，
∴AN=AM，
∵AD=AE，
∴Rt△ANE≌Rt△AMD（HL），
∴EN=DM，
∵∠ANG=∠NGD=∠AMG=90°，
AN=AM，
∴四邊形ANGM是正方形，
∴NG=GM，
∵A、B、C、G四點共圓，
∴∠GAC=∠GBC，∠ACG=∠ABG，
∵∠ABG=∠GBC，
∴∠GAC=∠ACG，
∴AG=CG，
∵△ANG是等腰直角三角形，
∴AG=$\sqrt{2}$NG，
∴CG=AG=$\sqrt{2}$NG，
∵EG+DG=EN+NG+MG-DM=NG+MG=2NG=2×$\frac{CG}{\sqrt{2}}$=$\sqrt{2}$CG．

點評 本題是三角形綜合題，考查了全等三角形的判定和性質、正方形的判定和性質、四點共圓等知識，解題的關鍵是靈活運用所學知識，學會添加常用輔助線，本題的難點是，四點共圓的應用，屬于中考壓軸題．