
分析 (1)利用分式的基本性質即可求出答案
(2)先將分子分母進行因式分解,然后再約分
(3)先將分子分母進行因式分解,然后去括號進行化簡運算.
解答 解:(1)原式=$\frac{2x-y}{x}$•$\frac{y}{-(2x-y)}$=-$\frac{y}{x}$
(2)原式=$\frac{2(a+3)}{{(a-2)}^{2}}$•$\frac{a-2}{a+3}$=$\frac{2}{a-2}$
(3)原式=($\frac{x+2}{x(x-2)}$-$\frac{x-1}{{(x-2)}^{2}}$)•$\frac{-x}{x-4}$
=$\frac{-(x+2)}{(x-2)(x-4)}$+$\frac{x(x-1)}{(x-2)^{2}(x-4)}$
=$-\frac{1}{{(x-2)}^{2}}$
點評 本題考查分式的混合運算,解題的關鍵是熟練運用分式的基本性質,本題屬于基礎題型.


 名校課堂系列答案
名校課堂系列答案科目:初中數學 來源: 題型:解答題
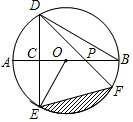 如圖,AB是⊙O的直徑,弦DE垂直平分半徑OA,C為垂足,弦DF與半徑OB相交于點P,連結EF、EO,若DE=2$\sqrt{3}$,∠DPA=45°.
如圖,AB是⊙O的直徑,弦DE垂直平分半徑OA,C為垂足,弦DF與半徑OB相交于點P,連結EF、EO,若DE=2$\sqrt{3}$,∠DPA=45°.查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
| A. | AB=CD,AD=BC | B. | AB∥CD,∠B=∠D | C. | ∠A=∠B,∠C=∠D | D. | AB=CD,∠BAC=∠ACD |
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
| A. | ①②③ | B. | ①④ | C. | ②③④ | D. | ①③ |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com