
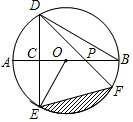
 如圖,AB是⊙O的直徑,弦DE垂直平分半徑OA,C為垂足,弦DF與半徑OB相交于點P,連結(jié)EF、EO,若DE=2$\sqrt{3}$,∠DPA=45°.
如圖,AB是⊙O的直徑,弦DE垂直平分半徑OA,C為垂足,弦DF與半徑OB相交于點P,連結(jié)EF、EO,若DE=2$\sqrt{3}$,∠DPA=45°.分析 (1)根據(jù)垂徑定理由OC⊥DE得EC=$\frac{1}{2}$DE=$\sqrt{3}$,由弦DE垂直平分半徑OA得OC=$\frac{1}{2}$OA=$\frac{1}{2}$OE,根據(jù)含30度的直角三角形三邊的關系得到∠E=30°,OC=$\frac{\sqrt{3}}{3}$CE=1,所以OE=2;
(2)連結(jié)OF,BF,BE,作BH⊥DF于H,如圖,根據(jù)圓周角定理得∠EOF=2∠EPF=90°;
(3))根據(jù)扇形面積公式和圖中陰影部分的面積=S扇形EOF-S△OEF計算得到S陰影=π-2.
解答 解:(1)∵OC⊥DE,
∴DC=EC=$\frac{1}{2}$DE=$\frac{1}{2}$×2$\sqrt{3}$=$\sqrt{3}$,
∵弦DE垂直平分半徑OA,
∴OC=$\frac{1}{2}$OA=$\frac{1}{2}$OE,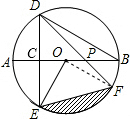
在Rt△OCE中,∵OE=2OC,
∴∠E=30°,
∴OC=$\frac{\sqrt{3}}{3}$CE=1,
∴OE=2,
即⊙O的半徑為2;
(2)連結(jié)OF,如圖,
∵∠DPA=45°,
∴∠DDC=45°,
∴∠EOF=2∠EPF=90°,
∴$\widehat{EF}$的長度=$\frac{90•π×2}{180}$=π;
(3)圖中陰影部分的面積=S扇形EOF-S△OEF
=$\frac{1}{2}$×π×2-$\frac{1}{2}$•2•2
=π-2.
點評 本題考查了垂徑定理:平分弦的直徑平分這條弦,并且平分弦所對的兩條弧.也考查了扇形的面積公式、圓周角定理和含30度的直角三角形三邊的關系.


 小學同步三練核心密卷系列答案
小學同步三練核心密卷系列答案科目:初中數(shù)學 來源: 題型:選擇題
| A. | 1個 | B. | 2個 | C. | 3個 | D. | 4個 |
查看答案和解析>>
科目:初中數(shù)學 來源: 題型:解答題
查看答案和解析>>
科目:初中數(shù)學 來源: 題型:選擇題
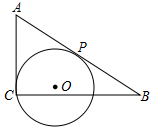 如圖,在Rt△ACB中,∠ACB=90°,AC=3,BC=4,有一過點C的動圓⊙O與斜邊AB相切于動點P,則⊙O的半徑r的最大值與最小值之差為( )
如圖,在Rt△ACB中,∠ACB=90°,AC=3,BC=4,有一過點C的動圓⊙O與斜邊AB相切于動點P,則⊙O的半徑r的最大值與最小值之差為( )| A. | $\frac{10}{3}$ | B. | $\frac{8}{5}$ | C. | $\frac{32}{15}$ | D. | $\frac{25}{12}$ |
查看答案和解析>>
科目:初中數(shù)學 來源: 題型:解答題
查看答案和解析>>
科目:初中數(shù)學 來源: 題型:解答題
查看答案和解析>>
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com