
| A. | AB=CD,AD=BC | B. | AB∥CD,∠B=∠D | C. | ∠A=∠B,∠C=∠D | D. | AB=CD,∠BAC=∠ACD |
分析 根據平行四邊形的判斷定理分別作出判斷得出即可.
解答 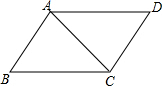 解:A、“AB=CD,AD=BC”是四邊形ABCD的兩組對邊分別相等,可以判定四邊形ABCD是平行四邊形,故本選項錯誤;
解:A、“AB=CD,AD=BC”是四邊形ABCD的兩組對邊分別相等,可以判定四邊形ABCD是平行四邊形,故本選項錯誤;
B、“AB∥CD,∠B=∠D”是四邊形ABCD的一組對邊平行,一組對角相等,不可以判定四邊形ABCD是平行四邊形,故本選項正確;
C、“∠A=∠C,∠B=∠D”是四邊形ABCD的兩組對角相等,可以判定四邊形ABCD是平行四邊形,故本選項錯誤;
B、“AB∥CD,AD=BC”是四邊形ABCD的一組對邊平行,另一組對邊相等,不可以判定四邊形ABCD是平行四邊形,故本選項錯誤;
D、由∠BAC=∠ACD可以推知AB∥CD,結合AB=CD,根據四邊形ABCD的一組對邊平行且相等,可以判定四邊形ABCD是平行四邊形,故本選項錯誤.
故選:B.
點評 此題主要考查了平行四邊形的判定定理,準確無誤的掌握定理是解題關鍵.


科目:初中數學 來源: 題型:選擇題
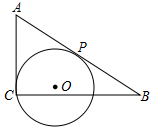 如圖,在Rt△ACB中,∠ACB=90°,AC=3,BC=4,有一過點C的動圓⊙O與斜邊AB相切于動點P,則⊙O的半徑r的最大值與最小值之差為( )
如圖,在Rt△ACB中,∠ACB=90°,AC=3,BC=4,有一過點C的動圓⊙O與斜邊AB相切于動點P,則⊙O的半徑r的最大值與最小值之差為( )| A. | $\frac{10}{3}$ | B. | $\frac{8}{5}$ | C. | $\frac{32}{15}$ | D. | $\frac{25}{12}$ |
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
| x | 1 | 2 | 3 |
| 代數式的值 | -2 | -5 | -8 |
| A. | x-3 | B. | 2x-10 | C. | 3x-17 | D. | -3x+1 |
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
 如圖,在⊙O中,半徑OA⊥OB,過OA的中點C作FD∥OB交⊙O于D、F兩點,且DF=2$\sqrt{3}$,以O為圓心,OC為半徑作弧CE,交OB于點E.
如圖,在⊙O中,半徑OA⊥OB,過OA的中點C作FD∥OB交⊙O于D、F兩點,且DF=2$\sqrt{3}$,以O為圓心,OC為半徑作弧CE,交OB于點E.查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com