
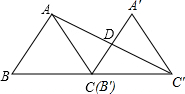
 如圖,已知三角形ABC的面積為12,將三角形ABC沿BC平移到三角形A′B′C′,使B′和C重合,連接AC′交A′C于D,D是A′C的中點,則三角形C′DC的面積為6.
如圖,已知三角形ABC的面積為12,將三角形ABC沿BC平移到三角形A′B′C′,使B′和C重合,連接AC′交A′C于D,D是A′C的中點,則三角形C′DC的面積為6. 分析 根據平移變換只改變圖形的位置,不改變圖形的形狀與大小,可得∠B=∠A′CC′,BC=B′C′,再根據同位角相等,兩直線平行可得CD∥AB,然后求出CD=$\frac{1}{2}$AB,點C′到A′C的距離等于點C到AB的距離,根據等高的三角形的面積的比等于底邊的比即可求解.
解答 解:根據題意得,∠B=∠A′CC′,BC=B′C′,
∴CD∥AB,CD=$\frac{1}{2}$AB(三角形的中位線),
∵點C′到A′C的距離等于點C到AB的距離,
∴△C′DC的面積=$\frac{1}{2}$△ABC的面積=$\frac{1}{2}$×12=6.
故答案為:6.
點評 本題考查了平移變換的性質,平行線的判定與性質,三角形的中位線等于第三邊的一半的性質,以及等高三角形的面積的比等于底邊的比,是小綜合題,但難度不大.


科目:初中數學 來源: 題型:解答題
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
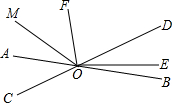 如圖,直線AB,CD相交于點O,∠DOE:∠BOE=3:1,OF平分∠AOD,
如圖,直線AB,CD相交于點O,∠DOE:∠BOE=3:1,OF平分∠AOD,查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com