Question

2．我們知道：光反射時，反射光線、入射光線和法線在同一平面內，反射光線、入射光線分別在法線兩側，反射角等于入射角．如圖，AO為入射光線，入射點為O，ON為法線（過入射點O且垂直于鏡面的直線），OB為反射光線，此時反射角∠BON等于入射角∠AON．


問題思考：
（1）如圖1，一束光線從點A處入射到平面鏡上，反射后恰好過點B，請在圖中確定平面鏡上的入射點P，保留作圖痕跡；
（2）如圖2，兩平面鏡OM、ON相交于點O，且OM⊥ON，一束光線從點A出發，經過平面鏡反射后，恰好經過點B．小昕說，光線可以只經過平面鏡OM反射后過點B，也可以只經過平面鏡ON反射后過點B．除了小昕的兩種做法外，你還有其它做法嗎？如果有，請在圖中畫出光線的行進路線，保留作圖痕跡；
問題拓展：
（3）如圖3，兩平面鏡OM、ON相交于點O，且∠MON=20°，一束光線從點P出發，經過若干次反射后，最后反射出去時，光線平行于平面鏡OM．設光線出發時與射線PM的夾角為θ（0°＜θ＜180°），請直接寫出滿足條件的所有θ的度數（注：OM、ON足夠長）

Answer 1

分析 （1）如圖1，作A關于平面鏡ML的對稱點A′，連接A′B交ML于點P，則點P即為所求，只要證明∠3=∠4即可．
（2）如圖2，作A關于OM的對稱點A′，作B關于ON的對稱點B′，連接A′B′分別交OM、ON于點P、Q．
（3）θ=40°，80°，120°，160°．分別作出圖形即可解決問題．

解答 解：（1）如圖1，作A關于平面鏡ML的對稱點A′，連接A′B交ML于點P，則點P即為所求．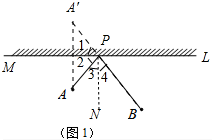

證明：如圖作PN⊥ML，
∵A與A′關于ML對稱，
∴∠1=∠2，
∵∠2+∠3=90°，∠1+∠2+∠3+∠4=180°，
∴∠1+∠4=90°，
∴∠3=∠4，
∴AP是入射光線，PB是反射光線，P即為入射點．

（2）如圖2，作A關于OM的對稱點A′，作B關于ON的對稱點B′，連接A′B′分別交OM、ON于點P、Q．
則光線的行進路線為A→P→Q→B．


（3）θ=40°，80°，120°，160°．理由如圖所示，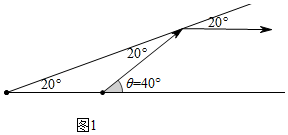

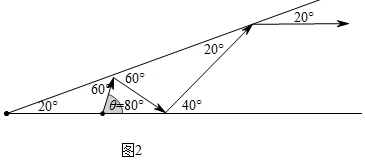
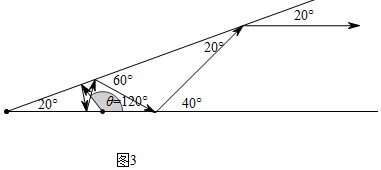
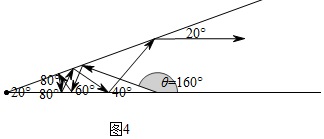
點評 本題考查軸對稱、翻折變換等知識，解題的關鍵是充分利用反射角等于入射角解決問題，第四個問題容易漏解，考慮問題要全面，屬于中考壓軸題．