Question

10．對任意x，y∈R，代數(shù)式M=$\sqrt{2{x}^{2}-6x+5}$+$\sqrt{{y}^{2}-4y+5}$+$\sqrt{2{x}^{2}-2xy+{y}^{2}}$的最小值為$\sqrt{10}$．

Answer 1

分析 可將不熟悉的“求三個二次根式和的最小值”的問題轉(zhuǎn)化為熟悉的“求三條線段和的最小值“的問題．若A的坐標為（1，2），B的坐標為（x，x），C的坐標為（y，0），D的坐標為（2，1），則根據(jù)勾股定理可得AB=$\sqrt{2{x}^{2}-6x+5}$，BC=$\sqrt{2{x}^{2}-2xy+{y}^{2}}$，CD=$\sqrt{{y}^{2}-4y+5}$，從而得到原式=AB+BC+CD，只需求出AB+BC+CD的最小值就可解決問題．

解答 解：如圖，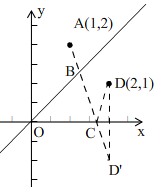
∵M=$\sqrt{2{x}^{2}-6x+5}$+$\sqrt{{y}^{2}-4y+5}$+$\sqrt{2{x}^{2}-2xy+{y}^{2}}$
=$\sqrt{（x-1）^{2}+（x-2）^{2}}$+$\sqrt{（y-2）^{2}+（0-1）^{2}}$+$\sqrt{（x-y）^{2}+（x-0）^{2}}$，
∴$\sqrt{（x-1）^{2}+（x-2）^{2}}$是點A（1，2）與點B（x，x）的距離，
$\sqrt{（y-2）^{2}+（0-1）^{2}}$是點C（y，0）與點D（2，1）的距離，
$\sqrt{（x-y）^{2}+（x-0）^{2}}$是點B（x，x）與C（y，0）的距離；
∴M=AB+BC+CD．
∵點B（x，x）在直線y=x上，點C（y，0）在x軸上，
作點D（2，1）關(guān)于x軸的對稱點D'（2，-1），
根據(jù)兩點之間線段最短可得：
當A、B、C、D'在同一條直線上時，AB+BC+CD=AB+BC+CD'最短，此時AB+BC+CD'的最小值等于AC+CD=AD'．
∵A（1，2），D'（2，-1），
∴AD'=$\sqrt{（1-2）^{2}+（2+1）^{2}}$=$\sqrt{10}$，
∴M=$\sqrt{2{x}^{2}-6x+5}$+$\sqrt{{y}^{2}-4y+5}$+$\sqrt{2{x}^{2}-2xy+{y}^{2}}$的最小值為$\sqrt{10}$，
故答案為：$\sqrt{10}$．

點評 本題主要考查了用待定系數(shù)法求一次函數(shù)的解析式、線段的垂直平分線的性質(zhì)、勾股定理、兩點之間線段最短等知識，考查了創(chuàng)造性思維和數(shù)形結(jié)合的思想，而把問題轉(zhuǎn)化為求線段和的最小值是解決本題的關(guān)鍵．