
 如圖,點A(a,b)在第一象限,AB⊥x軸于點B.C為邊0A的中點.在邊OB從小于AB到大于AB的變化過程中.若a+b的值始終保持不變,則在經過動點C的反比例函數y=$\frac{k}{x}$(k≠0)中k的值的變化情況是( )
如圖,點A(a,b)在第一象限,AB⊥x軸于點B.C為邊0A的中點.在邊OB從小于AB到大于AB的變化過程中.若a+b的值始終保持不變,則在經過動點C的反比例函數y=$\frac{k}{x}$(k≠0)中k的值的變化情況是( )| A. | 一直增大 | B. | 一直不變 | C. | 先增大后減小 | D. | 先減小后增大 |
分析 由點A在第一象限即可得出a+b>0、ab>0,根據反比例函數圖象上點的坐標特征結合點C的坐標即可得出k=$\frac{ab}{4}$,再根據(a-b)2≥0即可得出ab≤$\frac{(a+b)^{2}}{4}$(當a=b時取等號),結合a+b為定值即可得出k的值先增大后減小,此題得解.
解答 解:∵點A(a,b)在第一象限,
∴a>0,b>0,
∴a+b>0,ab>0.
∵點C為邊0A的中點,
∴點C的坐標為($\frac{a}{2}$,$\frac{b}{2}$).
∵點C在反比例函數y=$\frac{k}{x}$(k≠0)的圖象上,
∴k=$\frac{a}{2}$×$\frac{b}{2}$=$\frac{ab}{4}$.
∵(a-b)2≥0,
∴(a+b)2-4ab≥0,
∴ab≤$\frac{(a+b)^{2}}{4}$(當a=b時取等號).
∵a+b為定值,
∴當a=b時,ab最大,
∴k的值先增大后減小.
故選C.
點評 本題考查了反比例函數圖象上點的坐標特征以及完全平方公式,利用完全平方公式找出ab≤$\frac{(a+b)^{2}}{4}$(當a=b時取等號)是解題的關鍵.


科目:初中數學 來源: 題型:填空題
查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
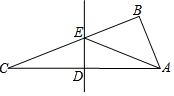 如圖,在△ABC中,∠ABC=90°,∠C=20°,DE是邊AC的垂直平分線,連結AE,則∠BAE等于( )
如圖,在△ABC中,∠ABC=90°,∠C=20°,DE是邊AC的垂直平分線,連結AE,則∠BAE等于( )| A. | 20° | B. | 40° | C. | 50° | D. | 70° |
查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
| A. | ($\frac{\sqrt{3}}{2}$,$\frac{1}{2}$) | B. | (-$\frac{1}{2}$,-$\frac{\sqrt{3}}{2}$) | C. | (-$\frac{\sqrt{3}}{2}$,$\frac{1}{2}$) | D. | (-$\frac{\sqrt{3}}{2}$,-$\frac{1}{2}$) |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com