
分析 可將求數20132014的末三位數字轉化為求數32014的末三位數字的問題,得20132014≡32014≡3100k+14≡314≡969;末三位從2的一次方開始:002,004,008,016,032,064,128,256,512,024,048,096,192,384,768,536,072,144,288,576,152,304,608,216,432,…504,008,因此找到一個規律就是:末三位由008的循環,即從2的3次方開始,到2的103次方,每100次出現末三位008的循環.因此969-3=966,966÷100余66,因此從008向后找13個即為536,依此即可求解.
解答 解:20132014≡32014≡3100k+14≡314≡969;
2012${\;}^{201{3}^{2014}}$≡2969,
末三位從2的一次方開始:002,004,008,016,032,064,128,256,512,024,048,096,192,384,768,536,072,144,288,576,152,304,608,216,432,…504,008,
規律就是:末三位由008的循環,即從2的3次方開始,到2的103次方,每100次出現末三位008的循環.
因此969-3=966,966÷100=9…66,
故2969的末三位數字是712.
故2012${\;}^{201{3}^{2014}}$的末三位數字是712.
點評 此題考查了尾數特征,解題的關鍵是從簡單的乘方運算開始,通過運算找出規律解決問題.


 名校課堂系列答案
名校課堂系列答案科目:初中數學 來源: 題型:填空題
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
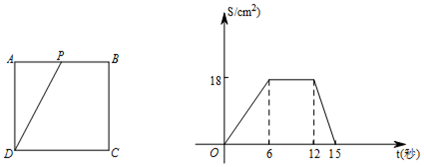
查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
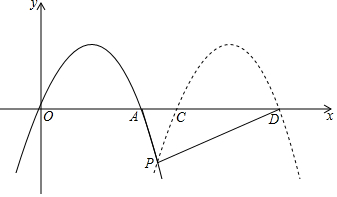 如圖,拋物線y=-2x2+4x與x軸的另一個交點為A,現將拋物線向右平移m(m>2)個單位長度,所得拋物線與x軸交于C,D,與原拋物線交于點P,設△PCD的面積為S,則用m表示S正確的是( )
如圖,拋物線y=-2x2+4x與x軸的另一個交點為A,現將拋物線向右平移m(m>2)個單位長度,所得拋物線與x軸交于C,D,與原拋物線交于點P,設△PCD的面積為S,則用m表示S正確的是( )| A. | $\frac{m}{2}$(m2-4) | B. | $\frac{1}{2}$m2-2 | C. | $\frac{m}{2}$(4-m2) | D. | 2-$\frac{1}{2}$m2 |
查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
| A. | 0 | B. | -1 | C. | 1 | D. | 2 |
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
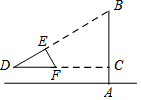 如圖,小南用自制的直角三角形紙板DEF測量樹的高度AB,他使斜邊DF保持水平,并且邊DE與點B在同一直線上.己知三角形的兩條直角邊DE=0.6m,EF=0.3m,測得邊DF離地面的高度AC=1.5m,CD=8m,求樹高AB.
如圖,小南用自制的直角三角形紙板DEF測量樹的高度AB,他使斜邊DF保持水平,并且邊DE與點B在同一直線上.己知三角形的兩條直角邊DE=0.6m,EF=0.3m,測得邊DF離地面的高度AC=1.5m,CD=8m,求樹高AB.查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
 如圖,點A(a,b)在第一象限,AB⊥x軸于點B.C為邊0A的中點.在邊OB從小于AB到大于AB的變化過程中.若a+b的值始終保持不變,則在經過動點C的反比例函數y=$\frac{k}{x}$(k≠0)中k的值的變化情況是( )
如圖,點A(a,b)在第一象限,AB⊥x軸于點B.C為邊0A的中點.在邊OB從小于AB到大于AB的變化過程中.若a+b的值始終保持不變,則在經過動點C的反比例函數y=$\frac{k}{x}$(k≠0)中k的值的變化情況是( )| A. | 一直增大 | B. | 一直不變 | C. | 先增大后減小 | D. | 先減小后增大 |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com