
分析 (1)由AC=7,BC=5,得到AB=2,由M是AB的中點,得到BM=1,于是得到結論;
(2)①C在線段AB上,求得CM=$\frac{1}{2}$(b-a),②點C在線段BA的延長線上,求得CM=AC+AM=a+$\frac{1}{2}$(b-a)=$\frac{1}{2}$(a+b).
解答 解:(1)∵AC=7,BC=5,
∴AB=2,
∵M是AB的中點,
∴BM=1,
∴CM=6,
故答案為:6;
(2)①C在線段AB上,
∵AC=a,BC=b,
∴AB=AC+BC=a+b,
∵點M是AB的中點,
∴BM=$\frac{1}{2}$AB=$\frac{1}{2}$(a+b),
∴CM=$\frac{1}{2}$(b-a),
②點C在線段BA的延長線上,
∵AC=a,BC=b,且a<b,
∴AB=b-a,
∵點M是AB的中點,
∴AM=$\frac{1}{2}$(b-a),
∴CM=AC+AM=a+$\frac{1}{2}$(b-a)=$\frac{1}{2}$(a+b),
故答案為:$\frac{1}{2}$(b-a)或$\frac{1}{2}$(a+b).
點評 本題考查了兩點間的距離,利用了線段的和差,線段中點的性質.


科目:初中數學 來源: 題型:解答題
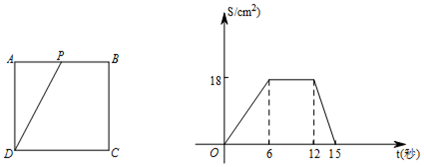
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
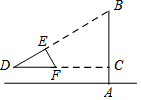 如圖,小南用自制的直角三角形紙板DEF測量樹的高度AB,他使斜邊DF保持水平,并且邊DE與點B在同一直線上.己知三角形的兩條直角邊DE=0.6m,EF=0.3m,測得邊DF離地面的高度AC=1.5m,CD=8m,求樹高AB.
如圖,小南用自制的直角三角形紙板DEF測量樹的高度AB,他使斜邊DF保持水平,并且邊DE與點B在同一直線上.己知三角形的兩條直角邊DE=0.6m,EF=0.3m,測得邊DF離地面的高度AC=1.5m,CD=8m,求樹高AB.查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
 據新華網消息,2016年6月20日,使用中國自主芯片制造的超級計算機“神威太湖之光”以浮點運算速度每秒930000000億次登上全球500強榜首,數字930000000用科學記數法可表示為( )
據新華網消息,2016年6月20日,使用中國自主芯片制造的超級計算機“神威太湖之光”以浮點運算速度每秒930000000億次登上全球500強榜首,數字930000000用科學記數法可表示為( )| A. | 9.3×108 | B. | 93×107 | C. | 0.93×109 | D. | 9.3×109 |
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
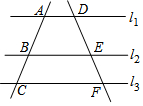 如圖,直線l1∥l2∥l3,直線AC依次交l1、l2、l3于A、B、C三點,直線DF依次交l1、l2、l3于D、E、F三點,若$\frac{AB}{AC}$=$\frac{4}{7}$,DE=2,求EF的長.
如圖,直線l1∥l2∥l3,直線AC依次交l1、l2、l3于A、B、C三點,直線DF依次交l1、l2、l3于D、E、F三點,若$\frac{AB}{AC}$=$\frac{4}{7}$,DE=2,求EF的長.查看答案和解析>>
科目:初中數學 來源: 題型:解答題
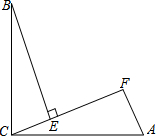 如圖,∠BCA=90°,AC=BC,BE⊥CF于點E,AF⊥CF于點F,其中0°<∠ACF<45°.
如圖,∠BCA=90°,AC=BC,BE⊥CF于點E,AF⊥CF于點F,其中0°<∠ACF<45°.查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
 如圖,點A(a,b)在第一象限,AB⊥x軸于點B.C為邊0A的中點.在邊OB從小于AB到大于AB的變化過程中.若a+b的值始終保持不變,則在經過動點C的反比例函數y=$\frac{k}{x}$(k≠0)中k的值的變化情況是( )
如圖,點A(a,b)在第一象限,AB⊥x軸于點B.C為邊0A的中點.在邊OB從小于AB到大于AB的變化過程中.若a+b的值始終保持不變,則在經過動點C的反比例函數y=$\frac{k}{x}$(k≠0)中k的值的變化情況是( )| A. | 一直增大 | B. | 一直不變 | C. | 先增大后減小 | D. | 先減小后增大 |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com