
分析 根據正比例函數y=4x與反比例函數y=$\frac{k}{x}$的圖象交于A、B兩點,點A坐標為(1,m),求得m=4×1=4,k=1×4=4,進而得出反比例函數為y=$\frac{4}{x}$,再設點P(m,$\frac{4}{m}$),分兩種情況進行討論:①P在AB右側,②P在AB左側,分別構造矩形,根據割補法列出關于m的方程,求得m的值,即可得到P點坐標.
解答 解:∵正比例函數y=4x與反比例函數y=$\frac{k}{x}$的圖象交于A、B兩點,點A坐標為(1,m),
∴m=4×1=4,k=1×4=4,
∴反比例函數為y=$\frac{4}{x}$,
設點P(m,$\frac{4}{m}$),
①當P在AB右側時,如圖所示,構造矩形BCDE,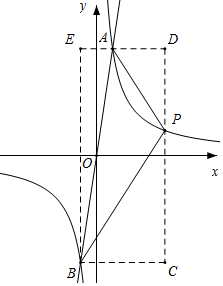
根據△ABP面積=矩形BCDE面積-△ABE面積-△BCP面積-△ADP面積,可得
8(m+1)-$\frac{1}{2}$×2×8-$\frac{1}{2}$×(m+1)×($\frac{4}{m}$+4)-$\frac{1}{2}$×(4-$\frac{4}{m}$)×(m-1)=40,
解得m=$\frac{5+3\sqrt{3}}{2}$或$\frac{5-3\sqrt{3}}{2}$,
∴$\frac{4}{m}$=-20+12$\sqrt{3}$或-20-12$\sqrt{3}$,
∴P($\frac{5+3\sqrt{3}}{2}$,-20+12$\sqrt{3}$)或($\frac{5-3\sqrt{3}}{2}$,-20-12$\sqrt{3}$);
②當P在AB左側時,如圖所示,構造矩形BCDE,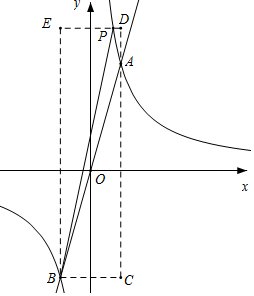
根據△ABP面積=矩形BCDE面積-△PBE面積-△BCA面積-△ADP面積,可得
2($\frac{4}{m}$+4)-$\frac{1}{2}$×(m+1)×($\frac{4}{m}$+4))-$\frac{1}{2}$×2×8-$\frac{1}{2}$×($\frac{4}{m}$-4)×(1-m)=40,
解得m=-5+$\sqrt{26}$或-5-$\sqrt{26}$,
∴$\frac{4}{m}$=20+4$\sqrt{26}$或20-4$\sqrt{26}$,
∴P(-5+$\sqrt{26}$,20+4$\sqrt{26}$)或(-5-$\sqrt{26}$,20-4$\sqrt{26}$).
點評 本題主要考查了反比例函數與一次函數交點的問題,解決問題的關鍵是作輔助線,構造矩形進行求解.解題時注意:若坐標平面內的三角形的各邊與坐標軸都不垂直時,需要運用割補法求解.


 閱讀快車系列答案
閱讀快車系列答案科目:初中數學 來源: 題型:填空題
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
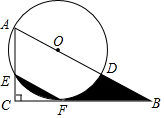 在Rt△ABC中,∠C=90°,D為AB邊上的一點,以AD為直徑的⊙O交AC于點E,交BC于點F,若F點恰好為$\widehat{DE}$的中點,連接EF、DF.
在Rt△ABC中,∠C=90°,D為AB邊上的一點,以AD為直徑的⊙O交AC于點E,交BC于點F,若F點恰好為$\widehat{DE}$的中點,連接EF、DF.查看答案和解析>>
科目:初中數學 來源: 題型:填空題

查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com