
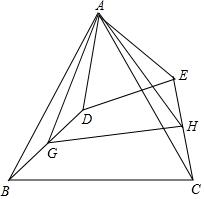
 如圖,△ABC中,AB=AC,∠BAC=α°(α為已知常數),以A為頂點作△ADE,使∠BAC=∠DAE,AD=AE,G、H分別為BD、CE的中點.
如圖,△ABC中,AB=AC,∠BAC=α°(α為已知常數),以A為頂點作△ADE,使∠BAC=∠DAE,AD=AE,G、H分別為BD、CE的中點.分析 (1)先證明△ABD≌△ACE,得∠ADB=∠AEC,BD=CE,再證明△ADG≌△AEH,可得結論;
(2)根據△ABD≌△ACE,得∠ABD=∠ACE,所以∠P=∠BAC=α°;
(3)如圖2中,作△ABC的外接圓,由(2)可知∠P=α=定值,推出點P在$\widehat{AC}$上運動,當點P′是優弧$\widehat{AB}$的中點P′時,點P′到AB的距離最大,作P′E⊥AB于E.求出P′E即可解決問題.
解答  證明:(1)∵∠BAC=∠DAE,
證明:(1)∵∠BAC=∠DAE,
∴∠BAD+∠DAC=∠EAC+∠DAC,
∴∠BAD=∠EAC,
∵AB=AC,AD=AE,
∴△ABD≌△ACE,
∴∠ADB=∠AEC,BD=CE,
∵G、H分別為BD、CE的中點,
∴DG=EH,
∴△ADG≌△AEH,
∴AG=AH,∠GAD=∠HAE,
∴∠GAD+∠DAH=∠HAE+∠DAH=α°,
即∠GAH=α°;
(2)如圖1,由(1)得:△ABD≌△ACE,
∴∠ABD=∠ACE,
∴∠ABD+∠DBC+∠ACB=∠DBC+∠ACB+∠ACE,
∴∠P=∠BAC=α°.
(3)如圖2中,作△ABC的外接圓,由(2)可知∠P=α=定值,
∴點P在$\widehat{AC}$上運動,當點P′是優弧$\widehat{AB}$的中點P′時,點P′到AB的距離最大,作P′E⊥AB于E.
∵$\widehat{AP′}$=$\widehat{BP′}$,P′E⊥AB,
∴P′A=P′B,AE=BE=$\frac{1}{2}$a,∠AP′E=′E=$\frac{1}{2}$∠AP′B=$\frac{1}{2}$∠ACB=$\frac{1}{2}$•$\frac{1}{2}$(180°-α)=45°-$\frac{1}{4}$α,
在Rt△AEP′中,tan∠AP′E=$\frac{AE}{P′E}$,
∴P′E=$\frac{\frac{1}{2}a}{tan(45°-\frac{1}{4}α)}$=$\frac{a}{2tan(45°-\frac{1}{4}α)}$.
點評 本題考查三角形綜合題、全等三角形的判定和性質、圓的有關知識,銳角三角函數,解直角三角形等知識,解題的關鍵是正確尋找全等三角形解決問題,重合添加輔助圓解決問題,屬于中考壓軸題.


科目:初中數學 來源: 題型:解答題

查看答案和解析>>
科目:初中數學 來源: 題型:解答題

查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
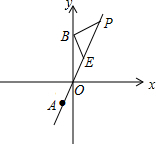 如圖,點A(-1,-2)為正比例函數y=kx的圖象上一點,B(0,4).
如圖,點A(-1,-2)為正比例函數y=kx的圖象上一點,B(0,4).查看答案和解析>>
科目:初中數學 來源: 題型:解答題
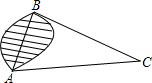 如圖,為了求出湖兩岸的A、B點之間的距離,一個觀測者在點C設樁,使三角形ABC恰好為直角三角形,通過測量,得到AC長160米,BC長128米,問從點A穿過湖到點B有多遠?
如圖,為了求出湖兩岸的A、B點之間的距離,一個觀測者在點C設樁,使三角形ABC恰好為直角三角形,通過測量,得到AC長160米,BC長128米,問從點A穿過湖到點B有多遠?查看答案和解析>>
科目:初中數學 來源: 題型:解答題
 如圖,已知在△ABC中,AD是BC邊上的中線,E是AD的中點,連接BE并延長交AC于點F,G是BF的中點.求證:
如圖,已知在△ABC中,AD是BC邊上的中線,E是AD的中點,連接BE并延長交AC于點F,G是BF的中點.求證:查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com