

分析 (1)以點A為圓心,AB長為半徑畫弧,交半圓于點E,連接AE,則根據SSS即可判定△ABO≌△AEO,進而得到∠ABO=∠AEO=90°,故AE是半圓的切線;
(2)根據AB、AE都是半圓的切線,即可得出AB=AE,再根據AB=BC,可得AE=BC,最后根據當AP∥CE時,CP<BC,即可得到CP<AE,進而得出結論.
解答 解:(1)如圖所示,AE即為所求;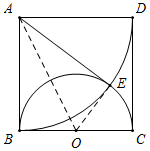
(2)如圖所示,四邊形APCE不能成為平行四邊形.
理由:∵AB、AE都是半圓的切線,
∴AB=AE,
又∵AB=BC,
∴AE=BC,
又∵當AP∥CE時,CP<BC,
∴CP<AE,
∴四邊形APCE不能成為平行四邊形.
點評 本題主要考查了復雜作圖,切線的性質,正方形的性質以及平行四邊形的判定,解決問題的關鍵是掌握:圓的切線垂直于經過切點的半徑.


 優加精卷系列答案
優加精卷系列答案科目:初中數學 來源: 題型:選擇題
| A. | 0.93×109 | B. | 9.3×108 | C. | 9.3×109 | D. | 93×107 |
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
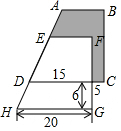 如圖所示,兩個完全相同的直角梯形重疊在一起,將其中一個直角梯形沿AD的方向平移,平移的距離為線段AE的長,求陰影部分的面積.(單位:cm)
如圖所示,兩個完全相同的直角梯形重疊在一起,將其中一個直角梯形沿AD的方向平移,平移的距離為線段AE的長,求陰影部分的面積.(單位:cm)查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
科目:初中數學 來源: 題型:填空題
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
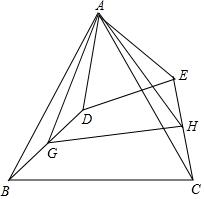 如圖,△ABC中,AB=AC,∠BAC=α°(α為已知常數),以A為頂點作△ADE,使∠BAC=∠DAE,AD=AE,G、H分別為BD、CE的中點.
如圖,△ABC中,AB=AC,∠BAC=α°(α為已知常數),以A為頂點作△ADE,使∠BAC=∠DAE,AD=AE,G、H分別為BD、CE的中點.查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com