
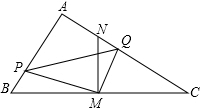
 如圖,在Rt△ABC中,∠BAC=90°,∠ABC=60°,AB=4$\sqrt{3}$,M是BC邊的中點,MN⊥BC交AC于點N.直角∠PMQ繞頂點M旋轉,使得邊MP于線段BA交于點P,邊MQ與線段AC交于點Q.
如圖,在Rt△ABC中,∠BAC=90°,∠ABC=60°,AB=4$\sqrt{3}$,M是BC邊的中點,MN⊥BC交AC于點N.直角∠PMQ繞頂點M旋轉,使得邊MP于線段BA交于點P,邊MQ與線段AC交于點Q.分析 (1)根據垂直的定義、同角的余角相等得到∠CNM=∠B,∠BMP=∠NMQ,根據相似三角形的判定定理證明即可;
(2)根據相似三角形的性質、直角三角形的性質用x表示出AQ、AP的長,根據三角形的面積公式計算即可;
(3)根據(2)的結論、結合圖形,運用函數思想進行計算即可.
解答 解:(1)△PBM與△QNM相似,
∵∠BAC=90°,
∴∠B+∠C=90°,
∵MN⊥BC,
∴∠CNM+∠C=90°,
∴∠CNM=∠B,
∵∠PMQ=90°,MN⊥BC,
∴∠BMP=∠NMQ,
∴△PBM∽△QNM;
(2)∵∠BAC=90°,∠ABC=60°,AB=4$\sqrt{3}$,
∴BC=8$\sqrt{3}$,AC=12,
∵M是BC邊的中點,
∴BM=MC=4$\sqrt{3}$,MN=4,NC=8,
∴AN=4,
∵△PBM∽△QNM,
∴$\frac{NQ}{BP}$=$\frac{MN}{BM}$,即$\frac{NQ}{x}$=$\frac{4}{4\sqrt{3}}$,
解得,NQ=$\frac{\sqrt{3}}{3}$x,
∴AQ=4+$\frac{\sqrt{3}}{3}$x,
∴S=$\frac{1}{2}$×AQ×AP=$\frac{1}{2}$×(4+$\frac{\sqrt{3}}{3}$x)×(4$\sqrt{3}$-x)
=-$\frac{\sqrt{3}}{6}$x2+8$\sqrt{3}$,0≤x<4$\sqrt{3}$;
(3)BP2+CQ2=PQ2,
證明:由(2)得,AQ=4+$\frac{\sqrt{3}}{3}$x,AP=4$\sqrt{3}$-x,
由勾股定理得,PQ2=AQ2+AP2=(4+$\frac{\sqrt{3}}{3}$x)2+(4$\sqrt{3}$-x)2
=$\frac{4}{3}$x2-$\frac{16}{3}$$\sqrt{3}$x+64,
CQ2=(8-$\frac{\sqrt{3}}{3}$x)2=$\frac{1}{3}$x2-$\frac{16}{3}\sqrt{3}$x+64,BP2=x2,
∴CQ2+BP2=$\frac{4}{3}$x2-$\frac{16}{3}$$\sqrt{3}$x+64,
∴BP2+CQ2=PQ2.
點評 本題考查的是相似三角形知識的綜合運用,掌握相似三角形的判定定理和性質定理是解題的關鍵,注意函數思想在解題中的靈活運用.


科目:初中數學 來源: 題型:選擇題
 如圖是用4個相同的小長方形與1個小正方形鑲嵌而成的圖案,已知該圖案的面積為25,小正方形的面積為4,若用x,y表示小長方形的兩鄰邊長(x>y),則下列關系中不正確的是( )
如圖是用4個相同的小長方形與1個小正方形鑲嵌而成的圖案,已知該圖案的面積為25,小正方形的面積為4,若用x,y表示小長方形的兩鄰邊長(x>y),則下列關系中不正確的是( )| A. | x+y=5 | B. | y-x=2 | C. | 4xy+4=25 | D. | y2+x2=25 |
查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
 如圖,在Rt△ABC中,∠C=90°,AD是∠BAC的平分線,AC=5,CD=3,則點D到AB的距離是( )
如圖,在Rt△ABC中,∠C=90°,AD是∠BAC的平分線,AC=5,CD=3,則點D到AB的距離是( )| A. | 2.5 | B. | 3 | C. | 4 | D. | 5 |
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
 如圖,從點O引出6條射線OA,OB,OC,OD,OE,OF,且∠AOB=100°,OF平分∠BOC,∠AOE=∠DOE,∠EOF=140°,求∠COD度數.
如圖,從點O引出6條射線OA,OB,OC,OD,OE,OF,且∠AOB=100°,OF平分∠BOC,∠AOE=∠DOE,∠EOF=140°,求∠COD度數.查看答案和解析>>
科目:初中數學 來源: 題型:解答題
 (1)如圖,點C在線段AB上,線段AC=6cm,BC=10cm,點D、E分別是AC和BC的中點.求線段DE的長;
(1)如圖,點C在線段AB上,線段AC=6cm,BC=10cm,點D、E分別是AC和BC的中點.求線段DE的長;查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com