
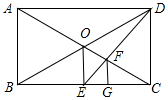
 如圖,在矩形ABCD中,對角線AC,BD相交于點O,OE⊥BC于點E,連接DE交OC于點F,作FG⊥BC于點G,則線段BG與GC的數量關系是BG=2CG.
如圖,在矩形ABCD中,對角線AC,BD相交于點O,OE⊥BC于點E,連接DE交OC于點F,作FG⊥BC于點G,則線段BG與GC的數量關系是BG=2CG. 分析 首先證明OE是△BDC的中位線,得到OE=$\frac{1}{2}$DC,由△EFO∽△DFC,可得$\frac{EO}{CD}$=$\frac{EF}{DF}$=$\frac{EG}{GC}$=$\frac{1}{2}$,設EG=a,則CG=2a,BE=EC=3a,推出BG=4a,CG=2a,由此即可解決問題.
解答  解:∵四邊形ABCD是矩形,
解:∵四邊形ABCD是矩形,
∴OB=OD,∠DCB=90°,
∵OE⊥BC,FG⊥BC,DC⊥BC,
∴OE∥FG∥CD,
∴BE=EC,△EFO∽△DFC,
∴OE=$\frac{1}{2}$CD,$\frac{EO}{CD}$=$\frac{EF}{DF}$=$\frac{EG}{GC}$=$\frac{1}{2}$,設EG=a,則CG=2a,BE=EC=3a,
∴BG=4a,CG=2a,
∴BG=2CG.
故答案為BG=2CG.
點評 本題考查矩形的性質、三角形中位線定理、平行線的性質等知識,解題的關鍵是靈活運用所學知識解決問題,學會利用參數解決問題,屬于中考常考題型.


 學習實踐園地系列答案
學習實踐園地系列答案科目:初中數學 來源: 題型:填空題
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
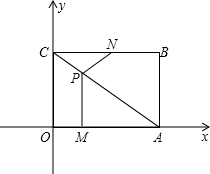 如圖,平面直角坐標系中,四邊形OABC為矩形,點A,B的坐標分別為(4,0),(4,3),動點M,N分別從O,B同時出發.以每秒1個單位的速度運動.其中,點M沿OA向終點A運動,點N沿BC向終點C運動.其中,點M沿OA向終點A運動,點N沿BN向終點C運動.過點M作MP⊥OA,交AC于P,連接NP,設M、N運動的時間為t秒(0<t<4).
如圖,平面直角坐標系中,四邊形OABC為矩形,點A,B的坐標分別為(4,0),(4,3),動點M,N分別從O,B同時出發.以每秒1個單位的速度運動.其中,點M沿OA向終點A運動,點N沿BC向終點C運動.其中,點M沿OA向終點A運動,點N沿BN向終點C運動.過點M作MP⊥OA,交AC于P,連接NP,設M、N運動的時間為t秒(0<t<4).查看答案和解析>>
科目:初中數學 來源: 題型:填空題
查看答案和解析>>
科目:初中數學 來源: 題型:填空題
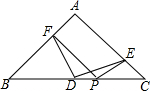 如圖,Rt△ABC中,∠BAC=90°,AB=AC,D為BC的中點,P為BC上一點,PF⊥AB于F,PE⊥AC于E,則DF與DE的關系為DF=DE且DF⊥ED.
如圖,Rt△ABC中,∠BAC=90°,AB=AC,D為BC的中點,P為BC上一點,PF⊥AB于F,PE⊥AC于E,則DF與DE的關系為DF=DE且DF⊥ED.查看答案和解析>>
科目:初中數學 來源: 題型:解答題
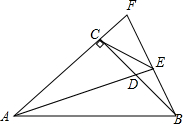 如圖,在△ABC中,∠ACB=90°,AC=BC,AD為△ABC的角平分線,過點B作AD的垂線,分別交AD、AC的延長線于E、F兩點,連接CE.
如圖,在△ABC中,∠ACB=90°,AC=BC,AD為△ABC的角平分線,過點B作AD的垂線,分別交AD、AC的延長線于E、F兩點,連接CE.查看答案和解析>>
科目:初中數學 來源: 題型:解答題
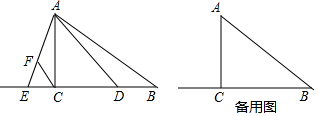
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com