
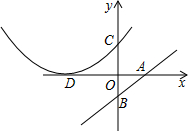
 如圖,直線AB的函數表達式為y=$\frac{m}{4}$x-m(m≠0,m為常數),點A、B分別在x軸、y軸上,tan∠OAB=$\frac{3}{4}$,點B關于x軸的對稱點為點C,以D(-6,0)為頂點的拋物線經過點C.
如圖,直線AB的函數表達式為y=$\frac{m}{4}$x-m(m≠0,m為常數),點A、B分別在x軸、y軸上,tan∠OAB=$\frac{3}{4}$,點B關于x軸的對稱點為點C,以D(-6,0)為頂點的拋物線經過點C.分析 (1)首先求出A、B、C坐標,根據頂點坐標,設拋物線的解析式為y=a(x+6)2,把C(0,3)代入求出a即可.
(2)分兩種情形討論,①當點P在原點O左邊,滿足$\frac{OP}{OA}$=$\frac{OC}{OB}$時,△POC∽△AOB,②當點P在原點O左邊,滿足$\frac{OP}{OB}$=$\frac{OC}{OA}$時,△POC∽△BOA,
求出P1,P2后,再求出P3、P4即可.
(3)如圖2中,設Q[n,$\frac{1}{12}$(n+6)2],作QN⊥AB于N,QM∥BC交AB于M,則M(n,$\frac{3}{4}$n-3),首先說明△MQN的三個內角是固定不變的,欲求QN的最小值,只要求出QM的最小值即可,再根據QN的最小值=QM•cos∠MQN=QM•cos∠OAB計算即可.
解答 解:(1)∵直線AB的函數表達式為y=$\frac{m}{4}$x-m,
∴A(4,0),B(0,-m),
在Rt△AOB中,∵OA=4,tan∠OAB=$\frac{3}{4}$=$\frac{OB}{OA}$,
∴OB=3,m=3,
∴B(0,-3),
∵B、C關于x軸對稱,
∴C(0,3),
∵拋物線的頂點為(-6,0),
∴可以假設拋物線的解析式為y=a(x+6)2,把C(0,3)代入得a=$\frac{1}{12}$,
∴拋物線的解析式為y=$\frac{1}{12}$(x+6)2.
(2)如圖1中,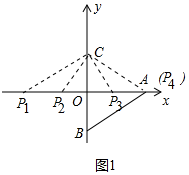
①當點P在原點O左邊,滿足$\frac{OP}{OA}$=$\frac{OC}{OB}$時,△POC∽△AOB,
∴$\frac{OP}{4}$=$\frac{3}{3}$,
∴OP=4,可得P1(-4,0).
②當點P在原點O左邊,滿足$\frac{OP}{OB}$=$\frac{OC}{OA}$時,△POC∽△BOA,
∴$\frac{OP}{3}$=$\frac{3}{4}$,
∴OP=$\frac{9}{4}$,可得P2(-$\frac{9}{4}$,0).
③根據對稱性可知當P3($\frac{9}{4}$,0),P4(4,0)時,也滿足條件.
綜上所述,滿足條件的點P坐標為(-4,0)或(-$\frac{9}{4}$,0)或(4,0)或($\frac{9}{4}$,0).
(3)如圖2中,設Q[n,$\frac{1}{12}$(n+6)2],作QN⊥AB于N,QM∥BC交AB于M,則M(n,$\frac{3}{4}$n-3),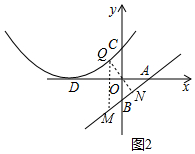
∵∠MQN+∠AMQ=90°,∠AMQ+∠BAO=90°,
∴∠MQN=∠BAO,
∴△MQN的三個內角是固定不變的,
∴欲求QN的最小值,只要求出QM的最小值即可,
∵QM=$\frac{1}{12}$(n+6)2-($\frac{3}{4}$n-3)=$\frac{1}{12}$(n+$\frac{3}{2}$)2+$\frac{93}{16}$,
∵$\frac{1}{12}$>0,
∴n=-$\frac{3}{2}$時,QM的最小值為$\frac{93}{16}$,
∴QN的最小值=QM•cos∠MQN=QM•cos∠OAB=$\frac{93}{16}$×$\frac{4}{5}$=$\frac{93}{20}$.
點評 本題考查二次函數的綜合題、相似三角形的判定和性質、銳角三角函數、勾股定理、待定系數法等知識,解題的關鍵是靈活運用首先知識,學會用轉化的思想思考問題,學會構建二次函數解決最值問題,第三個問題的關鍵是把求QN的最小值,轉化為求QM的最小值,屬于中考壓軸題.


 探究與鞏固河南科學技術出版社系列答案
探究與鞏固河南科學技術出版社系列答案科目:初中數學 來源: 題型:填空題
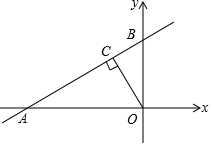 如圖,直線y=$\frac{\sqrt{3}}{3}$x+$\frac{4\sqrt{3}}{3}$與x軸、y軸分別交于A,B兩點,過點O作OC⊥AB于點C,點P是OA上的動點,若使△PAC為等腰三角形,則點P的坐標是(2$\sqrt{3}$-4,0)或(-2,0).
如圖,直線y=$\frac{\sqrt{3}}{3}$x+$\frac{4\sqrt{3}}{3}$與x軸、y軸分別交于A,B兩點,過點O作OC⊥AB于點C,點P是OA上的動點,若使△PAC為等腰三角形,則點P的坐標是(2$\sqrt{3}$-4,0)或(-2,0).查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
 如圖,AB、CD為⊙O的兩條弦,已知AB⊥CD于點E,OF⊥AB于點F,已知AC=4$\sqrt{5}$,
如圖,AB、CD為⊙O的兩條弦,已知AB⊥CD于點E,OF⊥AB于點F,已知AC=4$\sqrt{5}$,| A. | 3 | B. | 4 | C. | $\sqrt{17}$ | D. | 4$\sqrt{5}$ |
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
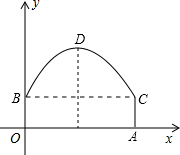 如圖,隧道的截面由拋物線和長方形構成,長方形的長OA為12m,寬OB為4m,建立直角坐標系,拋物線可用y=-$\frac{1}{6}$x2+bx+c表示.
如圖,隧道的截面由拋物線和長方形構成,長方形的長OA為12m,寬OB為4m,建立直角坐標系,拋物線可用y=-$\frac{1}{6}$x2+bx+c表示.查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
| A. | 畫一個三角形其內角和為361° | |
| B. | 任意做一個矩形,其對角線相等 | |
| C. | 任取一個實數,其相反數之和為0 | |
| D. | 外觀相同的10件同種產品中有2件是不合格產品,現從中抽取一件恰為合格品 |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com