
 如圖,AB、CD為⊙O的兩條弦,已知AB⊥CD于點E,OF⊥AB于點F,已知AC=4$\sqrt{5}$,
如圖,AB、CD為⊙O的兩條弦,已知AB⊥CD于點E,OF⊥AB于點F,已知AC=4$\sqrt{5}$,| A. | 3 | B. | 4 | C. | $\sqrt{17}$ | D. | 4$\sqrt{5}$ |
分析 先根據圖1求直徑AP=2$\sqrt{65}$,則半徑的長為$\sqrt{65}$;再利用圖2,作輔助線,構建矩形和直角三角形,利用勾股定理求DG的長,設OF=x,AF=a,分別表示出AE、BE、DE、CE的長,根據△AEC∽△DEB,列比例式得方程組,解出即可求OF的長,最后利用勾股定理求OE的長.
解答  解:如圖1,作直徑AP,連接CP、BP,AC,
解:如圖1,作直徑AP,連接CP、BP,AC,
∵AP是直徑,
∴∠ACP=∠ABP=90°,
∴PB⊥AB,
又∵AB⊥CD,
∴BP∥CD,
∴$\widehat{CP}=\widehat{BD}$,
∴CP=BD,
根據勾股定理,得:AC2+BD2=AC2+CP2=AP2,
∴AP=$\sqrt{A{C}^{2}+B{D}^{2}}$=2$\sqrt{65}$,
如圖2,過O作OG⊥CD于G,連接OD,則DG=CG,
設OF=x,AF=a,則AE=a+1,BE=a-1,
∵∠OFE=∠AED=∠OGE=90°,
∴四邊形OGEF是矩形,
∴OG=EF=1,EG=OF=x,
在Rt△OGD中,OD=$\frac{1}{2}$×$2\sqrt{65}$=$\sqrt{65}$,
由勾股定理得:DG=$\sqrt{O{D}^{2}-O{G}^{2}}$=$\sqrt{(\sqrt{65})^{2}-{1}^{2}}$=8,
∴DG=CG=8,
∴DE=8+x,CE=8-x,
∵∠AEC=∠DEB,∠C=∠B,
∴△AEC∽△DEB,
∴$\frac{AC}{BD}=\frac{AE}{DE}$=$\frac{EC}{EB}$,
∴$\frac{4\sqrt{5}}{6\sqrt{5}}$=$\frac{a+1}{8+x}$=$\frac{8-x}{a-1}$,
則$\left\{\begin{array}{l}{16+2x=3a+3}\\{2a-2=24-3x}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{x=4}\\{a=7}\end{array}\right.$,
∴OF=4,
在Rt△OEF中,EF=1,
由勾股定理得:OE=$\sqrt{O{F}^{2}+E{F}^{2}}$=$\sqrt{{4}^{2}+{1}^{2}}$=$\sqrt{17}$;
故選C.
點評 本題是圓的綜合題,考查了垂徑定理、勾股定理、圓周角定理;明確各定理的內容并能靈活應用是關鍵,另外本題還通過輔助線,構建直徑,利用直徑所對的圓周角為直角建立直角三角形,利用勾股定理和相似三角形列等式,并與方程組結合,解決問題.


科目:初中數學 來源: 題型:解答題
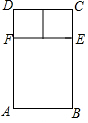 如圖是一種窗框的設計示意圖,矩形ABCD被分成上下兩部分,上部的矩形CDFE由兩個正方形組成,制作窗框的材料總長為6m.
如圖是一種窗框的設計示意圖,矩形ABCD被分成上下兩部分,上部的矩形CDFE由兩個正方形組成,制作窗框的材料總長為6m.查看答案和解析>>
科目:初中數學 來源: 題型:填空題
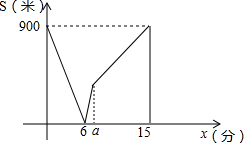 甲、乙兩人在筆直的路上勻速行走,甲從A地步行前往B地,乙從B地步行前往A地,甲、乙兩人同時出發,甲先到達B地后原地休息,甲、乙兩人之間的距離S(米)與乙步行的時間t(分)之間的函數關系的圖象如圖所示,則a=10分鐘.
甲、乙兩人在筆直的路上勻速行走,甲從A地步行前往B地,乙從B地步行前往A地,甲、乙兩人同時出發,甲先到達B地后原地休息,甲、乙兩人之間的距離S(米)與乙步行的時間t(分)之間的函數關系的圖象如圖所示,則a=10分鐘.查看答案和解析>>
科目:初中數學 來源: 題型:解答題
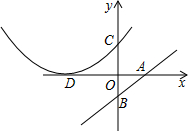 如圖,直線AB的函數表達式為y=$\frac{m}{4}$x-m(m≠0,m為常數),點A、B分別在x軸、y軸上,tan∠OAB=$\frac{3}{4}$,點B關于x軸的對稱點為點C,以D(-6,0)為頂點的拋物線經過點C.
如圖,直線AB的函數表達式為y=$\frac{m}{4}$x-m(m≠0,m為常數),點A、B分別在x軸、y軸上,tan∠OAB=$\frac{3}{4}$,點B關于x軸的對稱點為點C,以D(-6,0)為頂點的拋物線經過點C.查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
| A. | 擴大為原來的3倍 | B. | 縮小為原來的$\frac{1}{3}$ | C. | 沒有變化 | D. | 不能確定 |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com