
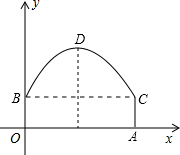
 如圖,隧道的截面由拋物線和長方形構成,長方形的長OA為12m,寬OB為4m,建立直角坐標系,拋物線可用y=-$\frac{1}{6}$x2+bx+c表示.
如圖,隧道的截面由拋物線和長方形構成,長方形的長OA為12m,寬OB為4m,建立直角坐標系,拋物線可用y=-$\frac{1}{6}$x2+bx+c表示.分析 (1)根據題意得出點B(0,4)、C(12,4),再利用待定系數法求解可得;
(2)根據題意求出x=6-4=2時的函數值,比較可得;
(3)兩排燈的距離不小于4$\sqrt{3}$,即每排燈到對稱軸的距離為2$\sqrt{3}$,據此可得求得x=6+2$\sqrt{3}$時的函數值,即可得答案.
解答 解:(1)根據題意將點B(0,4)、C(12,4)代入解析式得:
$\left\{\begin{array}{l}{c=4}\\{-\frac{1}{6}×144+12b+c=4}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{b=2}\\{c=4}\end{array}\right.$,
∴y=-$\frac{1}{6}$x2+2x+4=-$\frac{1}{6}$(x-6)2+10,
∴拱頂D到地面OA的距離為10m;
(2)∵當x=6-4=2時,y=-$\frac{1}{6}$(x-6)2+10=-$\frac{1}{6}$×16+10=$\frac{22}{3}$>6,
∴如果隧道內設雙向行車道,那么這輛貨車能安全通過;
(3)根據題意知,當x=6+2$\sqrt{3}$時,y=-$\frac{1}{6}$×(2$\sqrt{3}$)2+10=8,
∴要使兩排燈的距離不小于4$\sqrt{3}$,那么兩排燈的高度最高是8米.
點評 本題考查了二次函數的應用:構建二次函數模型解決實際問題,利用二次函數解決拋物線形的隧道、大橋和拱門等實際問題時,要恰當地把這些實際問題中的數據落實到平面直角坐標系中的拋物線上,從而確定拋物線的解析式,通過解析式可解決一些測量問題或其他問題.


科目:初中數學 來源: 題型:選擇題
| A. | (2,6) | B. | (1,1.5) | C. | (-1,1.5) | D. | (2,8) |
查看答案和解析>>
科目:初中數學 來源: 題型:填空題
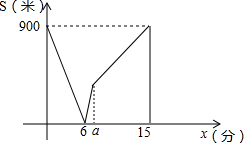 甲、乙兩人在筆直的路上勻速行走,甲從A地步行前往B地,乙從B地步行前往A地,甲、乙兩人同時出發,甲先到達B地后原地休息,甲、乙兩人之間的距離S(米)與乙步行的時間t(分)之間的函數關系的圖象如圖所示,則a=10分鐘.
甲、乙兩人在筆直的路上勻速行走,甲從A地步行前往B地,乙從B地步行前往A地,甲、乙兩人同時出發,甲先到達B地后原地休息,甲、乙兩人之間的距離S(米)與乙步行的時間t(分)之間的函數關系的圖象如圖所示,則a=10分鐘.查看答案和解析>>
科目:初中數學 來源: 題型:解答題
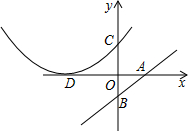 如圖,直線AB的函數表達式為y=$\frac{m}{4}$x-m(m≠0,m為常數),點A、B分別在x軸、y軸上,tan∠OAB=$\frac{3}{4}$,點B關于x軸的對稱點為點C,以D(-6,0)為頂點的拋物線經過點C.
如圖,直線AB的函數表達式為y=$\frac{m}{4}$x-m(m≠0,m為常數),點A、B分別在x軸、y軸上,tan∠OAB=$\frac{3}{4}$,點B關于x軸的對稱點為點C,以D(-6,0)為頂點的拋物線經過點C.查看答案和解析>>
科目:初中數學 來源: 題型:解答題
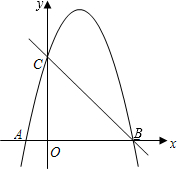 如圖,已知拋物線y=ax2+bx-5a經過點(-1,0),C(0,5)兩點,與x軸交于另一點B.
如圖,已知拋物線y=ax2+bx-5a經過點(-1,0),C(0,5)兩點,與x軸交于另一點B.查看答案和解析>>
科目:初中數學 來源: 題型:解答題
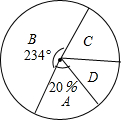 某中學為了科學建設“學生健康成長工程”,隨機抽取了部分學生家庭對其家長進行了主題“周末孩子在家您關心了嗎?”的調查問卷,將收回的調查問卷進行了分析整理,得到了如下的樣本統計圖表和扇形統計圖:
某中學為了科學建設“學生健康成長工程”,隨機抽取了部分學生家庭對其家長進行了主題“周末孩子在家您關心了嗎?”的調查問卷,將收回的調查問卷進行了分析整理,得到了如下的樣本統計圖表和扇形統計圖:| 代號 | 情況分類 | 家庭數 |
| A | 帶孩子玩且關心其作業完成情況 | 8 |
| B | 只關心其作業完成情況 | m |
| C | 只帶孩子玩 | 4 |
| D | 既不帶孩子玩也不關心其作業完成情況 | n |
查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
| A. | 1米 | B. | 2米 | C. | 4米 | D. | 5米 |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com