
| A. | (2,6) | B. | (1,1.5) | C. | (-1,1.5) | D. | (2,8) |
分析 先利用待定系數法求二次函數的解析式,再依次將各選項的點代入解析式即可作出判斷.
解答 解:把(-2,6)代入y=ax2(a≠0)中得:4a=6,
a=$\frac{3}{2}$,
∴這個二次函數的解析式為:y=$\frac{3}{2}{x}^{2}$,
A、當x=2時,y=$\frac{3}{2}$×22=6,所以點(2,6)在該函數的圖象上;
B、當x=1時,y=$\frac{3}{2}$×12=1.5,所以點(1,1.5)在該函數的圖象上;
C、當x=-1時,y=$\frac{3}{2}$×(-1)2=1.5,所以點(-1,1.5)在該函數的圖象上;
D、當x=2時,y=$\frac{3}{2}$×22=6,所以點(2,8)不在該函數的圖象上;
故選D.
點評 本題考查了利用待定系數求簡單的二次函數的解析式,以及判斷點是否在函數圖象上的方法,即代入解析式判斷是否滿足函數解析式.


 智能訓練練測考系列答案
智能訓練練測考系列答案科目:初中數學 來源: 題型:解答題
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
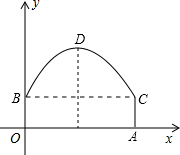 如圖,隧道的截面由拋物線和長方形構成,長方形的長OA為12m,寬OB為4m,建立直角坐標系,拋物線可用y=-$\frac{1}{6}$x2+bx+c表示.
如圖,隧道的截面由拋物線和長方形構成,長方形的長OA為12m,寬OB為4m,建立直角坐標系,拋物線可用y=-$\frac{1}{6}$x2+bx+c表示.查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com